Advertisements
Advertisements
Question
Using the information in the following figure, find its area.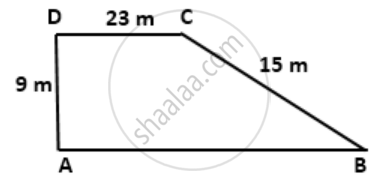
Solution
Construction : Draw CM ⊥ AB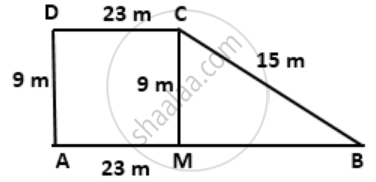
In right-angled triangle CMB,
BM2 = BC2 - CM2 = (15)2 - (9)2 = 225 - 81 = 144
⇒ BM = 12 m
Now, AB = AM + BM = 23 + 12 = 35 m
∴ Area of trapezium ABCD
=`1/2` x ( sum of parallel sides ) x Heigt
=`1/2` x (AB + CD) x AD
= `1/2` x ( 23 + 35 ) x 9
= `1/2` x 58 x 9
= 261 m2
APPEARS IN
RELATED QUESTIONS
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
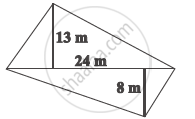
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
The distance between parallel sides of a trapezium is 15 cm and the length of the line segment joining the mid-points of its non-parallel sides is 26 cm. Find the area of the trapezium.
The length of a rectangle is twice the side of a square and its width is 6 cm greater than the side of the square. If the area of the rectangle is three times the area of the square; find the dimensions of each.
Trapezium given below; find its area.
A rectangular plot 85 m long and 60 m broad is to be covered with grass leaving 5 m all around. Find the area to be laid with grass.
The width of a rectangular room is `4/7`of its length, x, and its perimeter is y. Write an equation connecting x and y. Find the length of the room when the perimeter is 4400 cm.
The length of a rectangular verandah is 3 m more than its breadth. The numerical value of its area is equal to the numerical value of its perimeter.
(i) Taking x as the breadth of the verandah, write an equation in x that represents the above statement
(ii) Solve the equation obtained in (i) above and hence find the dimensions of the verandah.
The area of a rhombus is 216 sq. cm. If it's one diagonal is 24 cm; find:
(i) Length of its other diagonal,
(ii) Length of its side,
(iii) The perimeter of the rhombus.
Find the area of the quadrilateral whose vertices are at (– 9, 0), (– 8, 6), (– 1, – 2) and (– 6, – 3)
