Advertisements
Advertisements
Question
Trapezium given below; find its area.
Solution
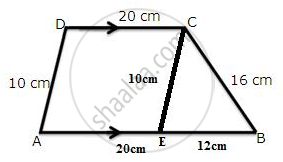
For the triangle EBC,
S = 19 cm
Area of ΔEBC = `sqrt( 19 xx ( 19 - 16 ) xx ( 19 - 12 ) xx ( 19 - 10 ))`
= `sqrt( 19 xx 3 xx 7 xx 9 )`
= 59.9 sq.cm
Let h be the height.
Area of ΔEBC= `1/2` x 12 x h
⇒ 59.9 = 6h
⇒ h = `59.9/6` = 9.98 cm
Area of ABCD = `1/2` x ( 20 + 32 ) x 9.98
= `1/2` x 52 x 9.98
= 259.48 cm2
APPEARS IN
RELATED QUESTIONS
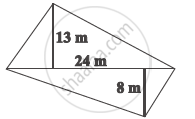
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
The area of a parallelogram is y cm2 and its height is h cm. The base of another parallelogram is x cm more than the base of the first parallelogram and its area is twice the area of the first. Find, in terms of y, h, and x, the expression for the height of the second parallelogram.
The perimeter of a rectangular board is 70 cm. Taking its length as x cm, find its width in terms of x.
If the area of the rectangular board is 300 cm2; find its dimensions.
Two adjacent sides of a parallelogram are 24 cm and 18 cm. If the distance between the longer sides is 12 cm; find the distance between the shorter sides.
A triangle and a parallelogram have the same base and the same area. If the side of the triangle is 26 cm, 28 cm, and 30 cm and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Vertices of given triangles are taken in order and their areas are provided aside. Find the value of ‘p’.
| Vertices | Area (sq.units) |
| (0, 0), (p, 8), (6, 2) | 20 |
In the following, find the value of ‘a’ for which the given points are collinear
(2, 3), (4, a) and (6, – 3)
Find the value of k, if the area of a quadrilateral is 28 sq. units, whose vertices are (– 4, – 2), (– 3, k), (3, – 2) and (2, 3)
Find the area of quadrilateral BCEG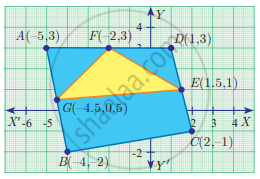
PQRS is a rectangle formed by joining the points P(– 1, – 1), Q(– 1, 4), R(5, 4) and S(5, – 1). A, B, C and D are the mid-points of PQ, QR, RS and SP respectively. Is the quadrilateral ABCD a square, a rectangle or a rhombus? Justify your answer.
