Advertisements
Advertisements
Question
The area of a parallelogram is y cm2 and its height is h cm. The base of another parallelogram is x cm more than the base of the first parallelogram and its area is twice the area of the first. Find, in terms of y, h, and x, the expression for the height of the second parallelogram.
Solution
Let 'y' and 'h' be the area and the height of the first parallelogram respectively.
Let 'height' be the height of the second parallelogram
base of the first parallelogram = `y/h`cm
the base of the second parallelogram = `( y/h + x )` cm
`( y/h + x )` x height = 2y
height = `[2hy]/[ y + hx ]`
APPEARS IN
RELATED QUESTIONS
The distance between parallel sides of a trapezium is 15 cm and the length of the line segment joining the mid-points of its non-parallel sides is 26 cm. Find the area of the trapezium.
The diagonals of a quadrilateral are 16 cm and 13 cm. If they intersect each other at right angles; find the area of the quadrilateral.
The area of a rectangular is 640 m2. Taking its length as x cm; find in terms of x, the width of the rectangle. If the perimeter of the rectangle is 104 m; find its dimensions.
A footpath of uniform width runs all around the outside of a rectangular field 30 m long and 24 m wide. If the path occupies an area of 360 m2, find its width.
The width of a rectangular room is `4/7`of its length, x, and its perimeter is y. Write an equation connecting x and y. Find the length of the room when the perimeter is 4400 cm.
The area of a rhombus is 216 sq. cm. If it's one diagonal is 24 cm; find:
(i) Length of its other diagonal,
(ii) Length of its side,
(iii) The perimeter of the rhombus.
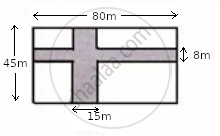
The diagram, given below, shows two paths drawn inside a rectangular field 80 m long and 45 m wide. The widths of the two paths are 8 m and 15 m as shown. Find the area of the shaded portion.
Find the area and the perimeter of a square with diagonal 24 cm. [Take √2 = 1.41 ]
Vertices of given triangles are taken in order and their areas are provided aside. Find the value of ‘p’.
| Vertices | Area (sq.units) |
| (p, p), (5, 6), (5, –2) | 32 |
Find the area of the quadrilateral whose vertices are at (– 9, – 2), (– 8, – 4), (2, 2) and (1, – 3)
