Advertisements
Advertisements
Question
The diagram, given below, shows two paths drawn inside a rectangular field 80 m long and 45 m wide. The widths of the two paths are 8 m and 15 m as shown. Find the area of the shaded portion.
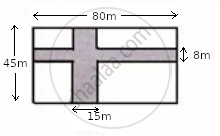
Solution
Consider the following figure.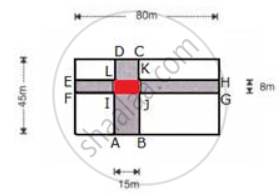
Thus, the area of the shaded portion
= Area( ABCD ) + Area( EFGH ) - Area( IJKL ) …(1)
Dimensions of ABCD: 45m × 15 m
Thus, the area of ABCD = 45 × 15 = 675 m2
Dimensions of EFGH: 80 m × 8 m
Thus, the area of EFGH = 80 × 8 = 640m2
Dimensions of IJKL: 15 m × 8 m
Thus, the area of IJKL = 15 × 8 = 120 m2
Therefore, from equation (1),
the area of the shaded portion = 675 + 640 - 120 = 1195 m2
APPEARS IN
RELATED QUESTIONS
Find the area of a quadrilateral one of whose diagonals is 30 cm long and the perpendiculars from the other two vertices are 19 cm and 11 cm respectively.
The area of a rectangular is 640 m2. Taking its length as x cm; find in terms of x, the width of the rectangle. If the perimeter of the rectangle is 104 m; find its dimensions.
Calculate the area of quadrilateral ABCD in which AB = 32 cm, AD = 24 cm ∠A = 90° and BC = CD = 52 cm.
The length and the breadth of a rectangle are 6 cm and 4 cm respectively. Find the height of a triangle whose base is 6 cm and the area is 3 times that of the rectangle.
The cost of enclosing a rectangular garden with a fence all around, at the rate of 75 paise per metre, is Rs. 300. If the length of the garden is 120 metres, find the area of the field in square metres.
The perimeter of a rhombus is 46 cm. If the height of the rhombus is 8 cm; find its area.
Two adjacent sides of a parallelogram are 28 cm and 26 cm. If one diagonal of it is 30 cm long; find the area of the parallelogram. Also, find the distance between its shorter sides.
Using the information in the following figure, find its area.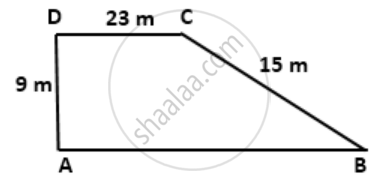
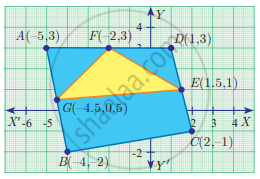
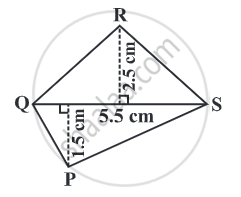
Find the area of quadrilateral PQRS.
Find the area of quadrilateral BCEG