Advertisements
Advertisements
Question
Two adjacent sides of a parallelogram are 28 cm and 26 cm. If one diagonal of it is 30 cm long; find the area of the parallelogram. Also, find the distance between its shorter sides.
Solution
At first, we have to calculate the area of the triangle having sides, then its perimeter 28 cm, 26 cm, and 30 cm.
Let a = 28, b = 26, c = 30
S = `[ 28 + 26 + 30 ]/2`
= `84/2`
= 42 cm
By Heron's Formula,
Area of a triangle = `sqrt[s( s - a )( s - b )( s - c )]`
= `sqrt[42( 42 - 28 )( 42 - 26 )( 42 - 30 )]`
= `sqrt( 42 xx 14 xx 16 xx 12)`
= `sqrt( 112896 )`
= 336 cm2
Area of a Parallelogram = 2 × Area of a triangle
= 2 × 336
= 672 cm2
We know that,
Area of a parallelogram = Height × Base
⇒ 672 = Height × 26
⇒ Height = 25.84 cm
∴ The distance between its shorter sides is 25.84 cm.
APPEARS IN
RELATED QUESTIONS
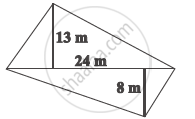
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
The distance between parallel sides of a trapezium is 15 cm and the length of the line segment joining the mid-points of its non-parallel sides is 26 cm. Find the area of the trapezium.
The length and the breadth of a rectangle are 6 cm and 4 cm respectively. Find the height of a triangle whose base is 6 cm and the area is 3 times that of the rectangle.
The cost of enclosing a rectangular garden with a fence all around, at the rate of 75 paise per metre, is Rs. 300. If the length of the garden is 120 metres, find the area of the field in square metres.
The perimeter of a rhombus is 52 cm. If one diagonal is 24 cm; find:
(i) The length of its other diagonal,
(ii) Its area.
Find the area and the perimeter of a square with diagonal 24 cm. [Take √2 = 1.41 ]
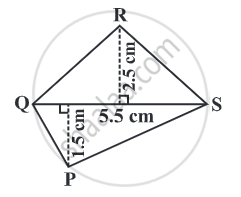
Find the area of quadrilateral PQRS.
The quadrilateral swimming pool shown is surrounded by concrete patio. Find the area of the patio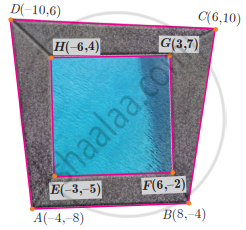
Find the area of quadrilateral BCEG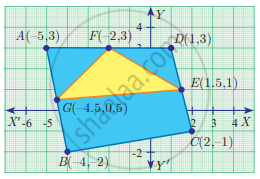
PQRS is a rectangle formed by joining the points P(– 1, – 1), Q(– 1, 4), R(5, 4) and S(5, – 1). A, B, C and D are the mid-points of PQ, QR, RS and SP respectively. Is the quadrilateral ABCD a square, a rectangle or a rhombus? Justify your answer.
