Advertisements
Advertisements
Question
Find the area and the perimeter of a square with diagonal 24 cm. [Take √2 = 1.41 ]
Solution
Diagonal of a square = 24 cm
Now, diagonal of a square = side of a square x `sqrt2`
⇒ 24 = side of a Square x `sqrt2`
⇒ Side of a square = `24/[sqrt2] = [12 xx sqrt2 xx sqrt2 ]/[sqrt2 ] = 12sqrt2`
∴ Area of a square = ( Side )2 = ( 12√2)2 = 288 cm2
And, perimeter of a square =
= 4 x Side
= 4 x 12`sqrt2`
= 48 x 1. 41
= 67. 68 cm.
APPEARS IN
RELATED QUESTIONS
The area of a parallelogram is y cm2 and its height is h cm. The base of another parallelogram is x cm more than the base of the first parallelogram and its area is twice the area of the first. Find, in terms of y, h, and x, the expression for the height of the second parallelogram.
The perimeter of a rectangular board is 70 cm. Taking its length as x cm, find its width in terms of x.
If the area of the rectangular board is 300 cm2; find its dimensions.
Trapezium given below; find its area.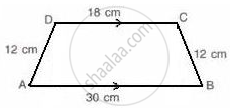
A wire when bent in the form of a square encloses an area of 484 m2. Find the largest area enclosed by the same wire when bent to from:
- An equilateral triangle.
- A rectangle of length 16 m.
The cost of enclosing a rectangular garden with a fence all around, at the rate of 75 paise per metre, is Rs. 300. If the length of the garden is 120 metres, find the area of the field in square metres.
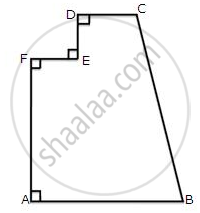
The figure given below shows the cross-section of a concrete structure. Calculate the area of cross-section if AB = 1.8 cm, CD = 0.6 m, DE = 0.8 m, EF = 0.3 m and AF = 1.2 m.
Two adjacent sides of a parallelogram are 28 cm and 26 cm. If one diagonal of it is 30 cm long; find the area of the parallelogram. Also, find the distance between its shorter sides.
Find the diagonal of a quadrilateral whose area is 756cm2 and the perpendicular from the opposite vertices are 17cm and 19cm.
In the following, find the value of ‘a’ for which the given points are collinear
(2, 3), (4, a) and (6, – 3)
If the diagonal d of a quadrilateral is doubled and the heights h1 and h2 falling on d are halved, then the area of quadrilateral is ______.
