Advertisements
Advertisements
Question
Sum of the areas of two squares is 400 cm2. If the difference of their perimeters is 16 cm, find the sides of the two squares.
Solution
Let the sides of two squares by a and b respectively.
Then, area of one square, S1 = a2
And, area of second square, S2 = b2
Given, S1 + S2 = 400 cm2
⇒ a2 + b2 = 400 cm2 …..(1)
Also, difference in perimeter = 16 cm
⇒ 4a - 4b = 16 cm
⇒ a - b = 4
⇒ a = (4 + b)
Substituting the value of 'a' in (1), we get
(4 + b)2 + b2 = 400
⇒ 16 + 8b + b2 + b2 = 400
⇒ 2b2 + 8b - 384 = 0
⇒ b2 + 4b - 192 = 0
⇒ b2 + 16b - 12b - 192 = 0
⇒ b(b + 16) - 12(b + 16) = 0
⇒ (b +16)(b - 12) = 0
⇒ b + 16 = 0 or b - 12 = 0
⇒ b = - 16 or b = 12
Since, the side of a square cannot be negative, we reject - 16.
Thus, b = 12
⇒ a = 4 + b = 4 + 12 = 16
Hence, the sides of a square are 16 cm and 12 cm respectively.
APPEARS IN
RELATED QUESTIONS
The area of a rectangular is 640 m2. Taking its length as x cm; find in terms of x, the width of the rectangle. If the perimeter of the rectangle is 104 m; find its dimensions.
Calculate the area of quadrilateral ABCD in which AB = 32 cm, AD = 24 cm ∠A = 90° and BC = CD = 52 cm.
The length and the breadth of a rectangle are 6 cm and 4 cm respectively. Find the height of a triangle whose base is 6 cm and the area is 3 times that of the rectangle.
A footpath of uniform width runs all around the outside of a rectangular field 30 m long and 24 m wide. If the path occupies an area of 360 m2, find its width.
The floor of a room is of size 6 m x 5 m. Find the cost of covering the floor of the room with 50 cm wide carpet at the rate of Rs.24.50 per metre. Also, find the cost of carpeting the same hall if the carpet, 60 cm, wide, is at the rate of Rs.26 per metre.
Vertices of given triangles are taken in order and their areas are provided aside. Find the value of ‘p’.
| Vertices | Area (sq.units) |
| (0, 0), (p, 8), (6, 2) | 20 |
Vertices of given triangles are taken in order and their areas are provided aside. Find the value of ‘p’.
| Vertices | Area (sq.units) |
| (p, p), (5, 6), (5, –2) | 32 |
The quadrilateral swimming pool shown is surrounded by concrete patio. Find the area of the patio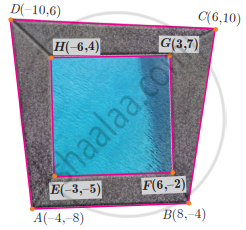
When proving that a quadrilateral is a parallelogram by using slopes you must find
If the diagonal d of a quadrilateral is doubled and the heights h1 and h2 falling on d are halved, then the area of quadrilateral is ______.
