Advertisements
Advertisements
प्रश्न
Sum of the areas of two squares is 400 cm2. If the difference of their perimeters is 16 cm, find the sides of the two squares.
उत्तर
Let the sides of two squares by a and b respectively.
Then, area of one square, S1 = a2
And, area of second square, S2 = b2
Given, S1 + S2 = 400 cm2
⇒ a2 + b2 = 400 cm2 …..(1)
Also, difference in perimeter = 16 cm
⇒ 4a - 4b = 16 cm
⇒ a - b = 4
⇒ a = (4 + b)
Substituting the value of 'a' in (1), we get
(4 + b)2 + b2 = 400
⇒ 16 + 8b + b2 + b2 = 400
⇒ 2b2 + 8b - 384 = 0
⇒ b2 + 4b - 192 = 0
⇒ b2 + 16b - 12b - 192 = 0
⇒ b(b + 16) - 12(b + 16) = 0
⇒ (b +16)(b - 12) = 0
⇒ b + 16 = 0 or b - 12 = 0
⇒ b = - 16 or b = 12
Since, the side of a square cannot be negative, we reject - 16.
Thus, b = 12
⇒ a = 4 + b = 4 + 12 = 16
Hence, the sides of a square are 16 cm and 12 cm respectively.
APPEARS IN
संबंधित प्रश्न
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
Find the area of a quadrilateral one of whose diagonals is 30 cm long and the perpendiculars from the other two vertices are 19 cm and 11 cm respectively.
Calculate the area of quadrilateral ABCD, in which ∠ABD = 90°, triangle BCD is an equilateral triangle of side 24 cm and AD = 26 cm.
The width of a rectangular room is `4/7`of its length, x, and its perimeter is y. Write an equation connecting x and y. Find the length of the room when the perimeter is 4400 cm.
The perimeter of a rhombus is 46 cm. If the height of the rhombus is 8 cm; find its area.
Two adjacent sides of a parallelogram are 24 cm and 18 cm. If the distance between the longer sides is 12 cm; find the distance between the shorter sides.
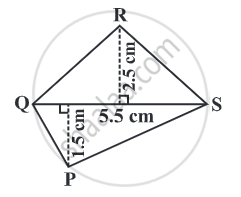
Find the area of quadrilateral PQRS.
In the following, find the value of ‘a’ for which the given points are collinear
(a, 2 – 2a), (– a + 1, 2a) and (– 4 – a, 6 – 2a)
Find the area of the quadrilateral whose vertices are at (– 9, – 2), (– 8, – 4), (2, 2) and (1, – 3)
If vertices of a quadrilateral are at A(– 5, 7), B(– 4, k), C(– 1, – 6) and D(4, 5) and its area is 72 sq. units. Find the value of k.
