Advertisements
Advertisements
प्रश्न
In the following, find the value of ‘a’ for which the given points are collinear
(a, 2 – 2a), (– a + 1, 2a) and (– 4 – a, 6 – 2a)
उत्तर
Let the points be A(a, 2 – 2a), B(– a + 1, 2a) C(– 4 – a, 6 – 2a).
Since the given points are collinear.
Area of a ∆ = 0
`1/2[(x_1y_2 + x_2y_3 + x_3y_1) - (x_2y_1 + x_3y_2 + x_1y_3)]` = 0

`1/2[((2"a"^2 + (- "a" + 1)(6 - 2"a") + (-4 - "a")(2 - 2"a"))), (-((- "a" + 1)(2 - 2"a") + 2"a"(-4 - "a") + (6 - 2"a")"a"))]` = 0
`1/2[((2"a"^2 - 6"a" + 2"a"^2 + 6 - 2"a" - 8 + 8"a" - 2"a" + 2"a"^2)-), ((-2"a" + 2"a"^2 + 2 - 2"a" - 8"a" - 2"a"^2 + 6"a" - 2"a"^2))]` = 0
`1/2[6"a"^2 - 10"a" + 8"a" - 2 - (2"a"^2 - 4"a"^2 - 12"a" + 6"a" + 2)]` = 0
6a2 – 2a – 2 – (– 2a2 – 6a + 2) = 0
6a2 – 2a – 2 + 2a2 + 6a – 2 = 0
8a2 + 4a – 4 = 0 ...(Divided by 4)
2a2 + a – 1 = 0
2a2 + 2a – a – 1 = 0
2a (a + 1) – 1 (a + 1) = 0
(a + 1) (2a – 1) = 0
a + 1 = 0 or 2a – 1 = 0
a = – 1 or 2a = 1 ⇒ a = `1/2`
The value of a = – 1 or `1/2`
APPEARS IN
संबंधित प्रश्न
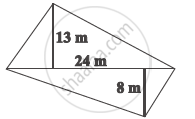
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
Find the area of a quadrilateral one of whose diagonals is 30 cm long and the perpendiculars from the other two vertices are 19 cm and 11 cm respectively.
Trapezium given below; find its area.
A footpath of uniform width runs all around the outside of a rectangular field 30 m long and 24 m wide. If the path occupies an area of 360 m2, find its width.
Two adjacent sides of a parallelogram are 28 cm and 26 cm. If one diagonal of it is 30 cm long; find the area of the parallelogram. Also, find the distance between its shorter sides.
The rate for a 1.20 m wide carpet is Rs. 40 per meter; find the cost of covering a hall 45 m long and 32 m wide with this carpet. Also, find the cost of carpeting the same hall if the carpet, 80 wide, is at Rs. 25. Per meter.
Find the area and perimeter of a square plot of land, the length of whose diagonal is 15 meters. Given your answer correct to 2 places of decimals.
The perimeter of a semicircular plate is 108 cm. find its area.
Find the area of the quadrilateral whose vertices are at (– 9, – 2), (– 8, – 4), (2, 2) and (1, – 3)
Find the value of k, if the area of a quadrilateral is 28 sq. units, whose vertices are (– 4, – 2), (– 3, k), (3, – 2) and (2, 3)
