Advertisements
Advertisements
प्रश्न
In the following, find the value of ‘a’ for which the given points are collinear
(a, 2 – 2a), (– a + 1, 2a) and (– 4 – a, 6 – 2a)
उत्तर
Let the points be A(a, 2 – 2a), B(– a + 1, 2a) C(– 4 – a, 6 – 2a).
Since the given points are collinear.
Area of a ∆ = 0
`1/2[(x_1y_2 + x_2y_3 + x_3y_1) - (x_2y_1 + x_3y_2 + x_1y_3)]` = 0

`1/2[((2"a"^2 + (- "a" + 1)(6 - 2"a") + (-4 - "a")(2 - 2"a"))), (-((- "a" + 1)(2 - 2"a") + 2"a"(-4 - "a") + (6 - 2"a")"a"))]` = 0
`1/2[((2"a"^2 - 6"a" + 2"a"^2 + 6 - 2"a" - 8 + 8"a" - 2"a" + 2"a"^2)-), ((-2"a" + 2"a"^2 + 2 - 2"a" - 8"a" - 2"a"^2 + 6"a" - 2"a"^2))]` = 0
`1/2[6"a"^2 - 10"a" + 8"a" - 2 - (2"a"^2 - 4"a"^2 - 12"a" + 6"a" + 2)]` = 0
6a2 – 2a – 2 – (– 2a2 – 6a + 2) = 0
6a2 – 2a – 2 + 2a2 + 6a – 2 = 0
8a2 + 4a – 4 = 0 ...(Divided by 4)
2a2 + a – 1 = 0
2a2 + 2a – a – 1 = 0
2a (a + 1) – 1 (a + 1) = 0
(a + 1) (2a – 1) = 0
a + 1 = 0 or 2a – 1 = 0
a = – 1 or 2a = 1 ⇒ a = `1/2`
The value of a = – 1 or `1/2`
APPEARS IN
संबंधित प्रश्न
The diagonal of a rectangular plot is 34 m and its perimeter is 92 m. Find its area.
The area of a rectangular is 640 m2. Taking its length as x cm; find in terms of x, the width of the rectangle. If the perimeter of the rectangle is 104 m; find its dimensions.
The following diagram shows a pentagonal field ABCDE in which the lengths of AF, FG, GH, and HD are 50 m, 40 m, 15 m and 25 m, respectively, and the lengths of perpendiculars BF, CH and EG are 50 m, 25 m and 60 m respectively. Determine the area of the field.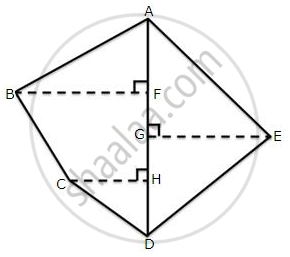
The width of a rectangular room is `4/7`of its length, x, and its perimeter is y. Write an equation connecting x and y. Find the length of the room when the perimeter is 4400 cm.
The perimeter of a rhombus is 46 cm. If the height of the rhombus is 8 cm; find its area.
The length of a rectangular verandah is 3 m more than its breadth. The numerical value of its area is equal to the numerical value of its perimeter.
(i) Taking x as the breadth of the verandah, write an equation in x that represents the above statement
(ii) Solve the equation obtained in (i) above and hence find the dimensions of the verandah.
Sum of the areas of two squares is 400 cm2. If the difference of their perimeters is 16 cm, find the sides of the two squares.
Vertices of given triangles are taken in order and their areas are provided aside. Find the value of ‘p’.
| Vertices | Area (sq.units) |
| (p, p), (5, 6), (5, –2) | 32 |
Find the value of k, if the area of a quadrilateral is 28 sq. units, whose vertices are (– 4, – 2), (– 3, k), (3, – 2) and (2, 3)
When proving that a quadrilateral is a trapezium, it is necessary to show
