Advertisements
Advertisements
प्रश्न
In the following, find the value of ‘a’ for which the given points are collinear
(2, 3), (4, a) and (6, – 3)
उत्तर
Let the points be A(2, 3), B(4, a) and C(6, – 3).
Since the given points are collinear.
Area of a triangle = 0
`1/2 [(x_1y_2 + x_2y_3 + x_3y_1) - (x_2y_1 + x_3y_2 + x_1y_3)]` = 0
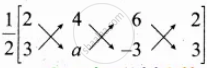
`1/2[(2"a" - 12 + 18) - (12 + 6"a" - 6)]` = 0
2a + 6 – (6 + 6a) = 0
2a + 6 – 6 – 6a = 0
– 4a = 0
⇒ a = `0/4`
= 0
The value of a = 0
APPEARS IN
संबंधित प्रश्न
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
The diagonal of a rectangular plot is 34 m and its perimeter is 92 m. Find its area.
Find the area of a quadrilateral one of whose diagonals is 30 cm long and the perpendiculars from the other two vertices are 19 cm and 11 cm respectively.
A rectangular plot of land measures 45 m x 30 m. A boundary wall of height 2.4 m is built all around the plot at a distance of 1 m from the plot. Find the area of the inner surface of the boundary wall.
ABCD is a square with each side 12 cm. P is a point on BC such that area of ΔABP: area of trapezium APCD = 1: 5. Find the length of CP.
The length of a rectangle is twice the side of a square and its width is 6 cm greater than the side of the square. If the area of the rectangle is three times the area of the square; find the dimensions of each.
Calculate the area of the figure given below: which is not drawn scale.
Find the area of the quadrilateral whose vertices are at (– 9, – 2), (– 8, – 4), (2, 2) and (1, – 3)
The quadrilateral swimming pool shown is surrounded by concrete patio. Find the area of the patio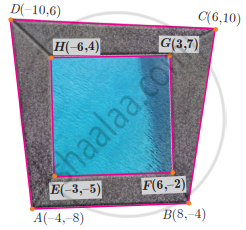
When proving that a quadrilateral is a trapezium, it is necessary to show
