Advertisements
Advertisements
प्रश्न
The quadrilateral swimming pool shown is surrounded by concrete patio. Find the area of the patio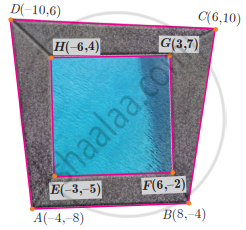
उत्तर
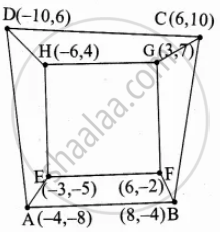
Area of the Quadrilateral ABCD = `1/2[(x_1y_2 + x_2y_3 + x_3y_4 + x_4y_1) - (x_2y_1 + x_3y_2 + x_4y_3 + x_1y_4)]`
= `1/2[(16 + 80 + 36 + 80) - (-64 - 24 - 100 - 24)]`
= `1/2[212 - (-212)]`

= `1/2[212 + 212]`
= `1/2[424]`
= 212 sq. units
Area of the Quadrilatera swimming pool EFGH = `1/2[(6 + 42 + 12 + 30) - (- 30 - 6 - 42 - 12)]`
= `1/2[90 - (- 90)]`
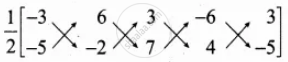
= `1/2[90 + 90]`
= `1/2 xx 180`
= 90 sq. units
Area of the patio = Area of the Quadrilateral ABCD – Area of the Quadrilateral EFGH
= (212 – 90) sq. units
Area of the patio = 122 sq. units
APPEARS IN
संबंधित प्रश्न
Trapezium given below; find its area.

Calculate the area of quadrilateral ABCD in which AB = 32 cm, AD = 24 cm ∠A = 90° and BC = CD = 52 cm.
A footpath of uniform width runs all around the outside of a rectangular field 30 m long and 24 m wide. If the path occupies an area of 360 m2, find its width.
The width of a rectangular room is `4/7`of its length, x, and its perimeter is y. Write an equation connecting x and y. Find the length of the room when the perimeter is 4400 cm.
A floor that measures 15 m x 8 m is to be laid with tiles measuring 50 cm x 25 cm. Find the number of tiles required.
Further, if a carpet is laid on the floor so that a space of 1 m exists between its edges and the edges of the floor, what fraction of the floor is left uncovered?
Find the area and perimeter of a square plot of land, the length of whose diagonal is 15 meters. Given your answer correct to 2 places of decimals.
A triangle and a parallelogram have the same base and the same area. If the side of the triangle is 26 cm, 28 cm, and 30 cm and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Sum of the areas of two squares is 400 cm2. If the difference of their perimeters is 16 cm, find the sides of the two squares.
The perimeter of a semicircular plate is 108 cm. find its area.
A quadrilateral field of unequal has a longer diagonal with 140m. The perpendiculars from opposite vertives upon this diagonal are 20m and 14m. Find the area of the field.
