Advertisements
Advertisements
प्रश्न
A footpath of uniform width runs all around the outside of a rectangular field 30 m long and 24 m wide. If the path occupies an area of 360 m2, find its width.
उत्तर
Let x be the width of the footpath.
Then
Area of footpath = `2 xx ( 30 + 24 )x + 4x^2`
= 4x2 + 108x
Again it is given that the area of the footpath is 360sq.m.
Hence,
4x2 + 108x = 360
x2 + 27x - 90 = 0
( x - 3 )( x + 30 ) = 0
x = 3
Hence width of the footpath is 3m.
APPEARS IN
संबंधित प्रश्न
The length of a rectangle is twice the side of a square and its width is 6 cm greater than the side of the square. If the area of the rectangle is three times the area of the square; find the dimensions of each.
The perimeter of a rectangular board is 70 cm. Taking its length as x cm, find its width in terms of x.
If the area of the rectangular board is 300 cm2; find its dimensions.
The perimeter of a rectangular field is `3/5`km. If the length of the field is twice its width; find the area of the rectangle in sq. meters.
The length and the breadth of a rectangle are 6 cm and 4 cm respectively. Find the height of a triangle whose base is 6 cm and the area is 3 times that of the rectangle.
The area of a rhombus is 216 sq. cm. If it's one diagonal is 24 cm; find:
(i) Length of its other diagonal,
(ii) Length of its side,
(iii) The perimeter of the rhombus.
Two adjacent sides of a parallelogram are 24 cm and 18 cm. If the distance between the longer sides is 12 cm; find the distance between the shorter sides.
The shaded region of the given diagram represents the lawn in the form of a house. On the three sides of the lawn, there are flowerbeds having a uniform width of 2 m.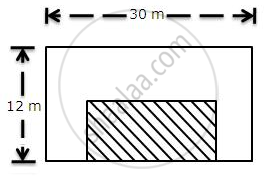
(i) Find the length and the breadth of the lawn.
(ii) Hence, or otherwise, find the area of the flower-beds.
Vertices of given triangles are taken in order and their areas are provided aside. Find the value of ‘p’.
| Vertices | Area (sq.units) |
| (0, 0), (p, 8), (6, 2) | 20 |
In the following, find the value of ‘a’ for which the given points are collinear
(2, 3), (4, a) and (6, – 3)
Let P(11, 7), Q(13.5, 4) and R(9.5, 4) be the midpoints of the sides AB, BC and AC respectively of ∆ABC. Find the coordinates of the vertices A, B and C. Hence find the area of ∆ABC and compare this with area of ∆PQR.
