Advertisements
Advertisements
प्रश्न
The perimeter of a rectangular board is 70 cm. Taking its length as x cm, find its width in terms of x.
If the area of the rectangular board is 300 cm2; find its dimensions.
उत्तर
Let b be the breadth of the rectangle. then its perimeter
2( x + b ) = 70
x + b = 35
b = 35 - x
Again
`x` x b = 300
x( 35 - x ) = 300
x2 - 35x + 300 = 0
( x - 15 )( x - 20 ) = 0
x = 15, 20.
Hence its length is 20 cm and width is 15 cm.
APPEARS IN
संबंधित प्रश्न
A wire when bent in the form of a square encloses an area = 576 cm2. Find the largest area enclosed by the same wire when bent to form;
(i) an equilateral triangle.
(ii) A rectangle whose adjacent sides differ by 4 cm.
Trapezium given below; find its area.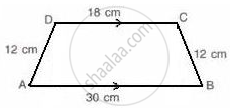
A footpath of uniform width runs all around the outside of a rectangular field 30 m long and 24 m wide. If the path occupies an area of 360 m2, find its width.
The perimeter of a rhombus is 46 cm. If the height of the rhombus is 8 cm; find its area.
The area of a rhombus is 216 sq. cm. If it's one diagonal is 24 cm; find:
(i) Length of its other diagonal,
(ii) Length of its side,
(iii) The perimeter of the rhombus.
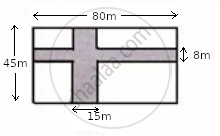
The diagram, given below, shows two paths drawn inside a rectangular field 80 m long and 45 m wide. The widths of the two paths are 8 m and 15 m as shown. Find the area of the shaded portion.
A triangle and a parallelogram have the same base and the same area. If the side of the triangle is 26 cm, 28 cm, and 30 cm and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Vertices of given triangles are taken in order and their areas are provided aside. Find the value of ‘p’.
| Vertices | Area (sq.units) |
| (p, p), (5, 6), (5, –2) | 32 |
In the following, find the value of ‘a’ for which the given points are collinear
(a, 2 – 2a), (– a + 1, 2a) and (– 4 – a, 6 – 2a)
When proving that a quadrilateral is a trapezium, it is necessary to show
