Advertisements
Advertisements
प्रश्न
A wire when bent in the form of a square encloses an area = 576 cm2. Find the largest area enclosed by the same wire when bent to form;
(i) an equilateral triangle.
(ii) A rectangle whose adjacent sides differ by 4 cm.
उत्तर
Let a be the length of each side.
a2 = 576
a = 24 cm
4a = 96 cm
Hence length of the wire = 96 cm
(i) For the equilateral triangle,
side = `96/3` = 32 cm
Area = `sqrt3/4`( side )2
= `sqrt3/4` x 322
= 256√3 sq.cm
(ii) Let the adjacent side of the rectangle be x and y cm.
Since the perimeter is 96 cm, we have,
2( x + y ) = 96
Hence,
x + y = 48
x - y = 4
x = 26
y = 22
Hence area of the rectangle is = 26 x 22 = 572 sq.cm
APPEARS IN
संबंधित प्रश्न
Find the area of a quadrilateral one of whose diagonals is 30 cm long and the perpendiculars from the other two vertices are 19 cm and 11 cm respectively.
ABCD is a square with each side 12 cm. P is a point on BC such that area of ΔABP: area of trapezium APCD = 1: 5. Find the length of CP.
The length of a rectangle is twice the side of a square and its width is 6 cm greater than the side of the square. If the area of the rectangle is three times the area of the square; find the dimensions of each.
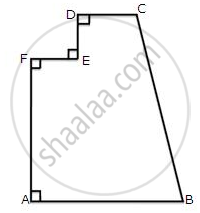
The figure given below shows the cross-section of a concrete structure. Calculate the area of cross-section if AB = 1.8 cm, CD = 0.6 m, DE = 0.8 m, EF = 0.3 m and AF = 1.2 m.
The length of a rectangular verandah is 3 m more than its breadth. The numerical value of its area is equal to the numerical value of its perimeter.
(i) Taking x as the breadth of the verandah, write an equation in x that represents the above statement
(ii) Solve the equation obtained in (i) above and hence find the dimensions of the verandah.
A quadrilateral field of unequal has a longer diagonal with 140m. The perpendiculars from opposite vertives upon this diagonal are 20m and 14m. Find the area of the field.
Find the area of a quadrilateral field whose sides are 12m, 9m, 18m and 21m respectively and the angle between the first two sides is a right angle. Take the value of `sqrt(6)` as 2.5.
Vertices of given triangles are taken in order and their areas are provided aside. Find the value of ‘p’.
| Vertices | Area (sq.units) |
| (0, 0), (p, 8), (6, 2) | 20 |
Find the value of k, if the area of a quadrilateral is 28 sq. units, whose vertices are (– 4, – 2), (– 3, k), (3, – 2) and (2, 3)
If the diagonal d of a quadrilateral is doubled and the heights h1 and h2 falling on d are halved, then the area of quadrilateral is ______.
