Advertisements
Advertisements
प्रश्न
If the diagonal d of a quadrilateral is doubled and the heights h1 and h2 falling on d are halved, then the area of quadrilateral is ______.
उत्तर
If the diagonal d of a quadrilateral is doubled and the heights h1 and h2 falling on d are halved, then the area of quadrilateral is `underlinebb(1/2(h_1 + h_2)d)`.
Explanation:
Let ABCD be a quadrilateral, where h1 and h2 are altitudes on the diagonal BD = d.
Then, area of quadrilateral ABCD = `1/2(h_1 + h_2) xx BD`
If altitudes are halved and the diagonal is doubled, then
Area of quadrilateral ABCD = `1/2(h_1/2 + h_2/2) xx 2d`
= `1/2((h_1 + h_2)/2) xx 2d`
= `1/2(h_1 + h_2) xx d`
APPEARS IN
संबंधित प्रश्न
A wire when bent in the form of a square encloses an area = 576 cm2. Find the largest area enclosed by the same wire when bent to form;
(i) an equilateral triangle.
(ii) A rectangle whose adjacent sides differ by 4 cm.
ABCD is a square with each side 12 cm. P is a point on BC such that area of ΔABP: area of trapezium APCD = 1: 5. Find the length of CP.
The length of a rectangle is twice the side of a square and its width is 6 cm greater than the side of the square. If the area of the rectangle is three times the area of the square; find the dimensions of each.
A footpath of uniform width runs all around the outside of a rectangular field 30 m long and 24 m wide. If the path occupies an area of 360 m2, find its width.
The perimeter of a rhombus is 46 cm. If the height of the rhombus is 8 cm; find its area.
The rate for a 1.20 m wide carpet is Rs. 40 per meter; find the cost of covering a hall 45 m long and 32 m wide with this carpet. Also, find the cost of carpeting the same hall if the carpet, 80 wide, is at Rs. 25. Per meter.
The shaded region of the given diagram represents the lawn in the form of a house. On the three sides of the lawn, there are flowerbeds having a uniform width of 2 m.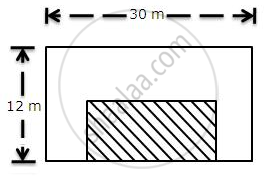
(i) Find the length and the breadth of the lawn.
(ii) Hence, or otherwise, find the area of the flower-beds.
In the following, find the value of ‘a’ for which the given points are collinear
(a, 2 – 2a), (– a + 1, 2a) and (– 4 – a, 6 – 2a)
When proving that a quadrilateral is a trapezium, it is necessary to show
When proving that a quadrilateral is a parallelogram by using slopes you must find
