Advertisements
Advertisements
प्रश्न
The shaded region of the given diagram represents the lawn in the form of a house. On the three sides of the lawn, there are flowerbeds having a uniform width of 2 m.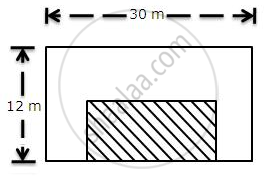
(i) Find the length and the breadth of the lawn.
(ii) Hence, or otherwise, find the area of the flower-beds.
उत्तर
Consider the following figure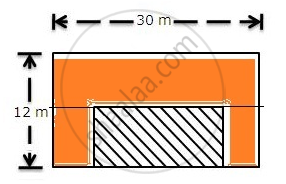
(i) The length of the lawn = 30 - 2 - 2 = 26 m
The breadth of the lawn = 12 - 2 = 10 m
(ii) The orange shaded area in the figure is the required area.
Area of the flower bed is calculated as follows:
A = 10 x 2 + 10 x 2 + 30 x 2
= 20 + 20 + 60
= 100 sq.m.
APPEARS IN
संबंधित प्रश्न
The diagonal of a rectangular plot is 34 m and its perimeter is 92 m. Find its area.
The area of a parallelogram is y cm2 and its height is h cm. The base of another parallelogram is x cm more than the base of the first parallelogram and its area is twice the area of the first. Find, in terms of y, h, and x, the expression for the height of the second parallelogram.
Find the area of a quadrilateral one of whose diagonals is 30 cm long and the perpendiculars from the other two vertices are 19 cm and 11 cm respectively.
The perimeter of a rectangular field is `3/5`km. If the length of the field is twice its width; find the area of the rectangle in sq. meters.
The length of a rectangular verandah is 3 m more than its breadth. The numerical value of its area is equal to the numerical value of its perimeter.
(i) Taking x as the breadth of the verandah, write an equation in x that represents the above statement
(ii) Solve the equation obtained in (i) above and hence find the dimensions of the verandah.
Two adjacent sides of a parallelogram are 24 cm and 18 cm. If the distance between the longer sides is 12 cm; find the distance between the shorter sides.
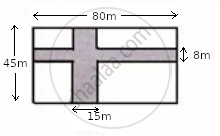
The diagram, given below, shows two paths drawn inside a rectangular field 80 m long and 45 m wide. The widths of the two paths are 8 m and 15 m as shown. Find the area of the shaded portion.
Find the area and the perimeter of a square with diagonal 24 cm. [Take √2 = 1.41 ]
When proving that a quadrilateral is a trapezium, it is necessary to show
If vertices of a quadrilateral are at A(– 5, 7), B(– 4, k), C(– 1, – 6) and D(4, 5) and its area is 72 sq. units. Find the value of k.
