Advertisements
Advertisements
प्रश्न
The perimeter of a rectangular field is `3/5`km. If the length of the field is twice its width; find the area of the rectangle in sq. meters.
उत्तर
Let the width be x and length 2x km.
Hence
`2 ( x + 2x ) = 3/5`
x = `1/10`km
= 100 m
Hence the width is 100m and length is 200m
The required area is given by
A = length x width
= 100 x 200
= 20,000 sq .m
APPEARS IN
संबंधित प्रश्न
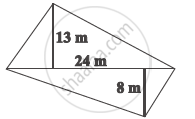
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
A rectangular plot of land measures 45 m x 30 m. A boundary wall of height 2.4 m is built all around the plot at a distance of 1 m from the plot. Find the area of the inner surface of the boundary wall.
The diagonals of a quadrilateral are 16 cm and 13 cm. If they intersect each other at right angles; find the area of the quadrilateral.
Calculate the area of quadrilateral ABCD in which AB = 32 cm, AD = 24 cm ∠A = 90° and BC = CD = 52 cm.
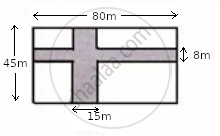
The diagram, given below, shows two paths drawn inside a rectangular field 80 m long and 45 m wide. The widths of the two paths are 8 m and 15 m as shown. Find the area of the shaded portion.
The rate for a 1.20 m wide carpet is Rs. 40 per meter; find the cost of covering a hall 45 m long and 32 m wide with this carpet. Also, find the cost of carpeting the same hall if the carpet, 80 wide, is at Rs. 25. Per meter.
A floor that measures 15 m x 8 m is to be laid with tiles measuring 50 cm x 25 cm. Find the number of tiles required.
Further, if a carpet is laid on the floor so that a space of 1 m exists between its edges and the edges of the floor, what fraction of the floor is left uncovered?
Find the area and perimeter of a square plot of land, the length of whose diagonal is 15 meters. Given your answer correct to 2 places of decimals.
Find the area of a quadrilateral field whose sides are 12m, 9m, 18m and 21m respectively and the angle between the first two sides is a right angle. Take the value of `sqrt(6)` as 2.5.
Find the area of the quadrilateral whose vertices are at (– 9, 0), (– 8, 6), (– 1, – 2) and (– 6, – 3)
