Advertisements
Advertisements
प्रश्न
The rate for a 1.20 m wide carpet is Rs. 40 per meter; find the cost of covering a hall 45 m long and 32 m wide with this carpet. Also, find the cost of carpeting the same hall if the carpet, 80 wide, is at Rs. 25. Per meter.
उत्तर
First, we have to calculate the area of the hall.
Area = 45 x 32
= 1440 m2
Cost = `40/1.20 xx 1440`
= 48,000
We need to find the cost of carpeting of 80 cm = 0.8 m wide carpet if the rate of carpeting is Rs. 25. Per meter.
Then
Cost = `25/0.8 xx 1440`
= Rs. 45,000
APPEARS IN
संबंधित प्रश्न
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
A wire when bent in the form of a square encloses an area = 576 cm2. Find the largest area enclosed by the same wire when bent to form;
(i) an equilateral triangle.
(ii) A rectangle whose adjacent sides differ by 4 cm.
ABCD is a square with each side 12 cm. P is a point on BC such that area of ΔABP: area of trapezium APCD = 1: 5. Find the length of CP.
Calculate the area of the figure given below: which is not drawn scale.
The floor of a room is of size 6 m x 5 m. Find the cost of covering the floor of the room with 50 cm wide carpet at the rate of Rs.24.50 per metre. Also, find the cost of carpeting the same hall if the carpet, 60 cm, wide, is at the rate of Rs.26 per metre.
Vertices of given triangles are taken in order and their areas are provided aside. Find the value of ‘p’.
| Vertices | Area (sq.units) |
| (0, 0), (p, 8), (6, 2) | 20 |
In the following, find the value of ‘a’ for which the given points are collinear
(a, 2 – 2a), (– a + 1, 2a) and (– 4 – a, 6 – 2a)
Find the area of quadrilateral BCEG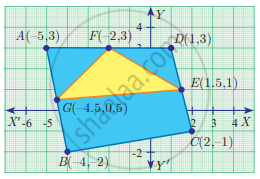
PQRS is a rectangle formed by joining the points P(– 1, – 1), Q(– 1, 4), R(5, 4) and S(5, – 1). A, B, C and D are the mid-points of PQ, QR, RS and SP respectively. Is the quadrilateral ABCD a square, a rectangle or a rhombus? Justify your answer.
If vertices of a quadrilateral are at A(– 5, 7), B(– 4, k), C(– 1, – 6) and D(4, 5) and its area is 72 sq. units. Find the value of k.
