Advertisements
Advertisements
प्रश्न
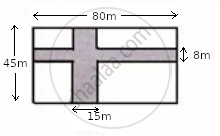
The diagram, given below, shows two paths drawn inside a rectangular field 80 m long and 45 m wide. The widths of the two paths are 8 m and 15 m as shown. Find the area of the shaded portion.
उत्तर
Consider the following figure.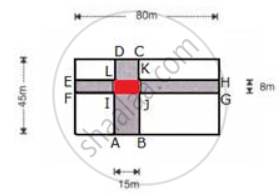
Thus, the area of the shaded portion
= Area( ABCD ) + Area( EFGH ) - Area( IJKL ) …(1)
Dimensions of ABCD: 45m × 15 m
Thus, the area of ABCD = 45 × 15 = 675 m2
Dimensions of EFGH: 80 m × 8 m
Thus, the area of EFGH = 80 × 8 = 640m2
Dimensions of IJKL: 15 m × 8 m
Thus, the area of IJKL = 15 × 8 = 120 m2
Therefore, from equation (1),
the area of the shaded portion = 675 + 640 - 120 = 1195 m2
APPEARS IN
संबंधित प्रश्न
A rectangular plot of land measures 45 m x 30 m. A boundary wall of height 2.4 m is built all around the plot at a distance of 1 m from the plot. Find the area of the inner surface of the boundary wall.
The length of a rectangle is twice the side of a square and its width is 6 cm greater than the side of the square. If the area of the rectangle is three times the area of the square; find the dimensions of each.
Trapezium given below; find its area.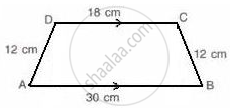
How many tiles, each of area 400 cm2, will be needed to pave a footpath which is 2 m wide and surrounds a grass plot 25 m long and 13 m wide?
The following diagram shows a pentagonal field ABCDE in which the lengths of AF, FG, GH, and HD are 50 m, 40 m, 15 m and 25 m, respectively, and the lengths of perpendiculars BF, CH and EG are 50 m, 25 m and 60 m respectively. Determine the area of the field.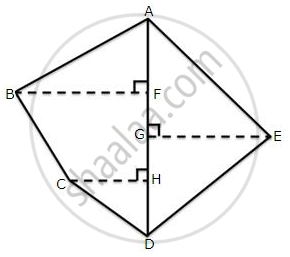
The cost of enclosing a rectangular garden with a fence all around, at the rate of 75 paise per metre, is Rs. 300. If the length of the garden is 120 metres, find the area of the field in square metres.
The perimeter of a rhombus is 52 cm. If one diagonal is 24 cm; find:
(i) The length of its other diagonal,
(ii) Its area.
Sum of the areas of two squares is 400 cm2. If the difference of their perimeters is 16 cm, find the sides of the two squares.
Find the area of a quadrilateral field whose sides are 12m, 9m, 18m and 21m respectively and the angle between the first two sides is a right angle. Take the value of `sqrt(6)` as 2.5.
In the following, find the value of ‘a’ for which the given points are collinear
(2, 3), (4, a) and (6, – 3)
