Advertisements
Advertisements
प्रश्न
The diagram, given below, shows two paths drawn inside a rectangular field 80 m long and 45 m wide. The widths of the two paths are 8 m and 15 m as shown. Find the area of the shaded portion.
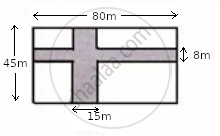
उत्तर
Consider the following figure.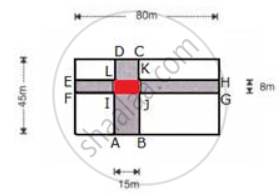
Thus, the area of the shaded portion
= Area( ABCD ) + Area( EFGH ) - Area( IJKL ) …(1)
Dimensions of ABCD: 45m × 15 m
Thus, the area of ABCD = 45 × 15 = 675 m2
Dimensions of EFGH: 80 m × 8 m
Thus, the area of EFGH = 80 × 8 = 640m2
Dimensions of IJKL: 15 m × 8 m
Thus, the area of IJKL = 15 × 8 = 120 m2
Therefore, from equation (1),
the area of the shaded portion = 675 + 640 - 120 = 1195 m2
APPEARS IN
संबंधित प्रश्न
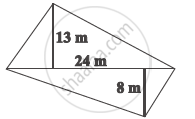
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
A rectangular plot of land measures 45 m x 30 m. A boundary wall of height 2.4 m is built all around the plot at a distance of 1 m from the plot. Find the area of the inner surface of the boundary wall.
The length of a rectangle is twice the side of a square and its width is 6 cm greater than the side of the square. If the area of the rectangle is three times the area of the square; find the dimensions of each.
The area of a rectangular is 640 m2. Taking its length as x cm; find in terms of x, the width of the rectangle. If the perimeter of the rectangle is 104 m; find its dimensions.
A wire when bent in the form of a square encloses an area of 484 m2. Find the largest area enclosed by the same wire when bent to from:
- An equilateral triangle.
- A rectangle of length 16 m.
Find the area and perimeter of a square plot of land, the length of whose diagonal is 15 meters. Given your answer correct to 2 places of decimals.
A triangle and a parallelogram have the same base and the same area. If the side of the triangle is 26 cm, 28 cm, and 30 cm and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
In the following, find the value of ‘a’ for which the given points are collinear
(2, 3), (4, a) and (6, – 3)
In the following, find the value of ‘a’ for which the given points are collinear
(a, 2 – 2a), (– a + 1, 2a) and (– 4 – a, 6 – 2a)
If vertices of a quadrilateral are at A(– 5, 7), B(– 4, k), C(– 1, – 6) and D(4, 5) and its area is 72 sq. units. Find the value of k.
