Advertisements
Advertisements
प्रश्न
A wire when bent in the form of a square encloses an area of 484 m2. Find the largest area enclosed by the same wire when bent to from:
- An equilateral triangle.
- A rectangle of length 16 m.
उत्तर
The area of the square is 484.
Let a be the length of each side of the square.
Now
a2 = 484
a = 22 m
Hence, the length of the wire is = 4 × 22 = 88 m.
(i) Now, this 88 m wire is bent in the form of an equilateral triangle.
Side of the triangle = `88/3`
= 29.3 m
Area of the triangle = `sqrt3/4` × (Side)2
= `sqrt3/4` × (29.3)2
= 372.58 m2
(ii) Let x be the breadth of the rectangle.
Now,
2(l + b) = 88
16 + x = 44
x = 28 m
Hence, area = 16 × 28 = 448 m2.
APPEARS IN
संबंधित प्रश्न
A rectangular plot 85 m long and 60 m broad is to be covered with grass leaving 5 m all around. Find the area to be laid with grass.
The following diagram shows a pentagonal field ABCDE in which the lengths of AF, FG, GH, and HD are 50 m, 40 m, 15 m and 25 m, respectively, and the lengths of perpendiculars BF, CH and EG are 50 m, 25 m and 60 m respectively. Determine the area of the field.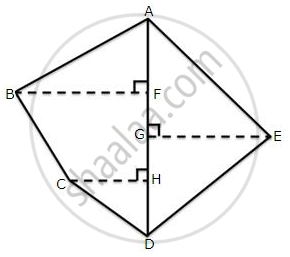
A quadrilateral field of unequal has a longer diagonal with 140m. The perpendiculars from opposite vertives upon this diagonal are 20m and 14m. Find the area of the field.
Find the diagonal of a quadrilateral whose area is 756cm2 and the perpendicular from the opposite vertices are 17cm and 19cm.
Vertices of given triangles are taken in order and their areas are provided aside. Find the value of ‘p’.
| Vertices | Area (sq.units) |
| (0, 0), (p, 8), (6, 2) | 20 |
Vertices of given triangles are taken in order and their areas are provided aside. Find the value of ‘p’.
| Vertices | Area (sq.units) |
| (p, p), (5, 6), (5, –2) | 32 |
Find the value of k, if the area of a quadrilateral is 28 sq. units, whose vertices are (– 4, – 2), (– 3, k), (3, – 2) and (2, 3)
Let P(11, 7), Q(13.5, 4) and R(9.5, 4) be the midpoints of the sides AB, BC and AC respectively of ∆ABC. Find the coordinates of the vertices A, B and C. Hence find the area of ∆ABC and compare this with area of ∆PQR.
Find the area of quadrilateral BCEG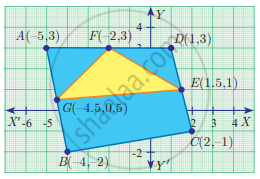
When proving that a quadrilateral is a trapezium, it is necessary to show
