Advertisements
Advertisements
प्रश्न
Let P(11, 7), Q(13.5, 4) and R(9.5, 4) be the midpoints of the sides AB, BC and AC respectively of ∆ABC. Find the coordinates of the vertices A, B and C. Hence find the area of ∆ABC and compare this with area of ∆PQR.
Advertisements
उत्तर
Let the vertices of the ∆ABC be A(x1, y1), B(x2, y2), C(x3, y3)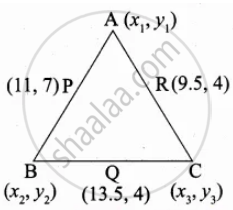
Mid point of AB = `((x_1 + x_2)/2, (y_1 + y_2)/2)`
(11, 7) = `((x_1 + x_2)/2, (y_1 + y_2)/2)`
|
`(x_1 + x_2)/2` = 11 x1 + x2 = 22 ...(1) |
`(y_1 + y_2)/2` = 7 y1 + y2 = 14 ...(2) |
Mid point of BC = `((x_2 + x_3)/2, (y_2 + y_3)/2)`
⇒ (13.5, 4) = `((x_2 + x_3)/2, (y_2 + y_3)/2)`
|
`(x_2 + x_3)/2` = 13.5 x2 + x3 = 27 ...(3) |
`(y_2 + y_3)/2` = 4 y2 + y3 = 8 ...(4) |
Mid point of AC = `((x_1 + x_3)/2, (y_1 + y_3)/2)`
(9.5, 4) = `((x_1 + x_2)/2, (y_1 + y_3)/2)`
|
`(x_1 + x_3)/2` = 9.5 x1 + x3 = 19 ...(5) |
`(y_1 + y_3)/2` = 4 y1 + y3 = 8 ...(6) |
Add (1), (3) and (5)
2x1 + 2x2 + 2x3 = 22 + 27 + 19
2(x1 + x2 + x3) = 68
x1 + x2 + x3 = 34
From (1) ⇒ x1 + x2 = 22
x3 = 34 – 22 = 12
From (3) ⇒ x2 + x3 = 27
x1 = 34 – 27 = 7
From (5) ⇒ x1 + x3 = 19
x2 = 34 – 19 = 15
Add (2), (4) and (6)
2y1 + 2y2 + 2y3 = 14 + 8 + 8
2(y1 + y2 + y3) = 30
y1 + y2 + y3 = 15
From (2) ⇒ y1 + y2 = 14
y3 = 15 – 14 = 1
From (4) ⇒ y2 + y3 = 18
y1 = 15 – 8 = 7
From (6) ⇒ y1 + y3 = 8
y2 = 15 – 8 = 7
The vertices of a ΔABC are A(7, 7), B(15, 7) and C(12, 1)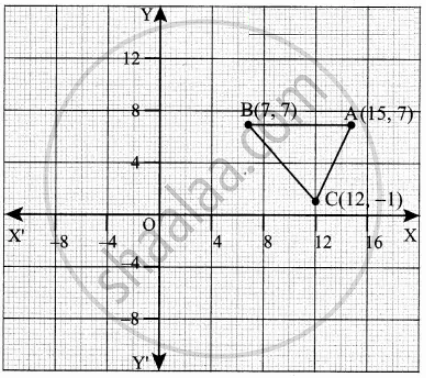
Area of ΔABC = `1/2[(x_1y_2 + x_2y_3 + x_3y_1) - (x_2y_1 + x_3y_2 + x_1y_3)]`
= `1/2[(7 + 84 + 105) - (84 + 15 + 49)]`
= `1/2[196 - 148]`
= `1/2 xx 48`
= 24 sq. units
Area of ΔPRQ = `1/2[(44 + 8 + 94.5) - (66.5 + 54 + 44)]`
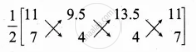
= `1/2[176.5 - 164.5]`
= `1/2 xx 12`
= 6 sq. units
APPEARS IN
संबंधित प्रश्न
Diagram of the adjacent picture frame has outer dimensions = 24 cm × 28 cm and inner dimensions 16 cm × 20 cm. Find the area of each section of the frame, if the width of each section is same.
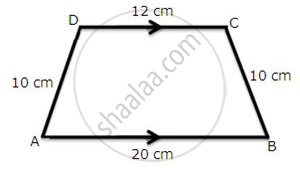
Calculate the area of quadrilateral ABCD, in which ∠ABD = 90°, triangle BCD is an equilateral triangle of side 24 cm and AD = 26 cm.
The perimeter of a rectangular field is `3/5`km. If the length of the field is twice its width; find the area of the rectangle in sq. meters.
A rectangular plot 85 m long and 60 m broad is to be covered with grass leaving 5 m all around. Find the area to be laid with grass.
The rate for a 1.20 m wide carpet is Rs. 40 per meter; find the cost of covering a hall 45 m long and 32 m wide with this carpet. Also, find the cost of carpeting the same hall if the carpet, 80 wide, is at Rs. 25. Per meter.
The shaded region of the given diagram represents the lawn in the form of a house. On the three sides of the lawn, there are flowerbeds having a uniform width of 2 m.
(i) Find the length and the breadth of the lawn.
(ii) Hence, or otherwise, find the area of the flower-beds.
Find the area and the perimeter of a square with diagonal 24 cm. [Take √2 = 1.41 ]
A quadrilateral field of unequal has a longer diagonal with 140m. The perpendiculars from opposite vertives upon this diagonal are 20m and 14m. Find the area of the field.
If vertices of a quadrilateral are at A(– 5, 7), B(– 4, k), C(– 1, – 6) and D(4, 5) and its area is 72 sq. units. Find the value of k.
If the diagonal d of a quadrilateral is doubled and the heights h1 and h2 falling on d are halved, then the area of quadrilateral is ______.
