Advertisements
Advertisements
प्रश्न
A triangle and a parallelogram have the same base and the same area. If the side of the triangle is 26 cm, 28 cm, and 30 cm and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
उत्तर
Let the sides of the triangle be
a = 26 cm, b = 28 cm and c = 30 cm
Now,
semi-perimeter of a triangle,
s = `( a + b + c )/( 2 ) = ( 26 + 28 + 30 )/(2 )= (84)/(2) = 42 cm`
∴ Area of triangle = `sqrt (s( s - a )( s - b )(s -c ))`
= `sqrt (42( 42 - 26 ) ( 42 - 28 ) (42 - 30 ))`
= `sqrt ( 42 xx 16 xx 14 xx 12 )`
= `sqrt( 7 xx 6 xx 4 xx 4 xx 7 xx 2 xx 6 xx 2)`
= `sqrt( 7 xx 7 xx 4 xx 4 xx 6 xx 6xx 2xx 2)`
= 7 x 4 x 6 x 2
= 336 cm2
Base of a parallelogram = 28 cm
Given ,
Area of parallelogram = Area of triangle
⇒ Base x Height = 336
⇒ 28 x Height = 336
⇒ Height = 12 cm
APPEARS IN
संबंधित प्रश्न
A rectangular plot of land measures 45 m x 30 m. A boundary wall of height 2.4 m is built all around the plot at a distance of 1 m from the plot. Find the area of the inner surface of the boundary wall.
The area of a rectangular is 640 m2. Taking its length as x cm; find in terms of x, the width of the rectangle. If the perimeter of the rectangle is 104 m; find its dimensions.
Trapezium given below; find its area.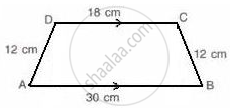
A rectangular plot 85 m long and 60 m broad is to be covered with grass leaving 5 m all around. Find the area to be laid with grass.
The length and the breadth of a rectangle are 6 cm and 4 cm respectively. Find the height of a triangle whose base is 6 cm and the area is 3 times that of the rectangle.
The following diagram shows a pentagonal field ABCDE in which the lengths of AF, FG, GH, and HD are 50 m, 40 m, 15 m and 25 m, respectively, and the lengths of perpendiculars BF, CH and EG are 50 m, 25 m and 60 m respectively. Determine the area of the field.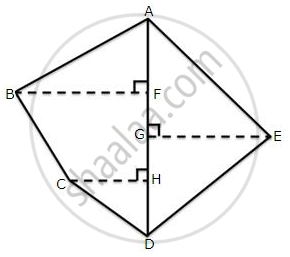
The length of a rectangular verandah is 3 m more than its breadth. The numerical value of its area is equal to the numerical value of its perimeter.
(i) Taking x as the breadth of the verandah, write an equation in x that represents the above statement
(ii) Solve the equation obtained in (i) above and hence find the dimensions of the verandah.
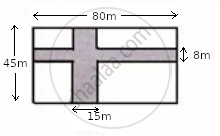
The diagram, given below, shows two paths drawn inside a rectangular field 80 m long and 45 m wide. The widths of the two paths are 8 m and 15 m as shown. Find the area of the shaded portion.
Find the area and the perimeter of a square with diagonal 24 cm. [Take √2 = 1.41 ]
Find the area of the quadrilateral whose vertices are at (– 9, 0), (– 8, 6), (– 1, – 2) and (– 6, – 3)
