Advertisements
Advertisements
Question
A triangle and a parallelogram have the same base and the same area. If the side of the triangle is 26 cm, 28 cm, and 30 cm and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Solution
Let the sides of the triangle be
a = 26 cm, b = 28 cm and c = 30 cm
Now,
semi-perimeter of a triangle,
s = `( a + b + c )/( 2 ) = ( 26 + 28 + 30 )/(2 )= (84)/(2) = 42 cm`
∴ Area of triangle = `sqrt (s( s - a )( s - b )(s -c ))`
= `sqrt (42( 42 - 26 ) ( 42 - 28 ) (42 - 30 ))`
= `sqrt ( 42 xx 16 xx 14 xx 12 )`
= `sqrt( 7 xx 6 xx 4 xx 4 xx 7 xx 2 xx 6 xx 2)`
= `sqrt( 7 xx 7 xx 4 xx 4 xx 6 xx 6xx 2xx 2)`
= 7 x 4 x 6 x 2
= 336 cm2
Base of a parallelogram = 28 cm
Given ,
Area of parallelogram = Area of triangle
⇒ Base x Height = 336
⇒ 28 x Height = 336
⇒ Height = 12 cm
APPEARS IN
RELATED QUESTIONS
The perimeter of a rectangular board is 70 cm. Taking its length as x cm, find its width in terms of x.
If the area of the rectangular board is 300 cm2; find its dimensions.
Calculate the area of quadrilateral ABCD in which AB = 32 cm, AD = 24 cm ∠A = 90° and BC = CD = 52 cm.
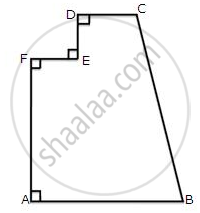
Calculate the area of the figure given below: which is not drawn scale.
The figure given below shows the cross-section of a concrete structure. Calculate the area of cross-section if AB = 1.8 cm, CD = 0.6 m, DE = 0.8 m, EF = 0.3 m and AF = 1.2 m.
The perimeter of a rhombus is 46 cm. If the height of the rhombus is 8 cm; find its area.
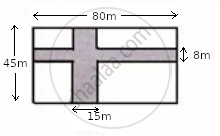
The diagram, given below, shows two paths drawn inside a rectangular field 80 m long and 45 m wide. The widths of the two paths are 8 m and 15 m as shown. Find the area of the shaded portion.
A floor that measures 15 m x 8 m is to be laid with tiles measuring 50 cm x 25 cm. Find the number of tiles required.
Further, if a carpet is laid on the floor so that a space of 1 m exists between its edges and the edges of the floor, what fraction of the floor is left uncovered?
Using the information in the following figure, find its area.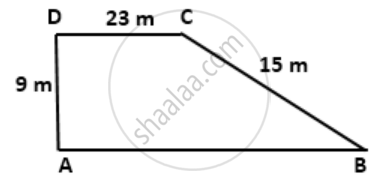
Find the area of the quadrilateral whose vertices are at (– 9, – 2), (– 8, – 4), (2, 2) and (1, – 3)
Find the area of the quadrilateral whose vertices are at (– 9, 0), (– 8, 6), (– 1, – 2) and (– 6, – 3)
