Advertisements
Advertisements
प्रश्न
Trapezium given below; find its area.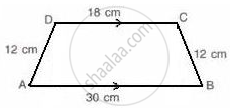
उत्तर
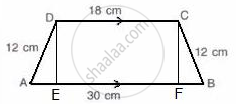
In the given figure, we can observe that the non-parallel sides are equal and hence it is an isosceles trapezium.
Therefore, let us draw DE and CF perpendiculars to AB.
Thus, the area of the parallelogram is given by
AB = AE + EF + FB and CD = EF = 18 cm, we have
30 = AE + 18 + FB
⇒ 30 = AE + 18 + AE
⇒ 2AE + 18 = 30
⇒ 2AE = 30 - 18
⇒ 2AE = 12
⇒ AE = 6 cm
Now, consider the right angled triangle ADE.
AD2 = AE2 + DE2
⇒ 122 = 62 + DE2
⇒ 144 = 36 + DE2
⇒ DE2 = 144 - 36
⇒ DE2 = 108
⇒ DE = `sqrt( 36 xx 3 )`
⇒ DE = `6sqrt3`
Area( `square"ABCD" ) = "Area"( Δ"ADE" ) + "Area"( square "DEFC") + "Area"( Δ"CFB" )`
⇒ Area( `square"ABCD" ) = 1/2 xx 6 xx 6sqrt3 + 18 xx 6sqrt3 + 1/2 xx 6 xx 6sqrt3`
⇒ Area( `square"ABCD" ) = 6 xx 6sqrt3 + 18 xx 6sqrt3`
⇒ Area( `square"ABCD") = 144sqrt3`= 249.41 cm2
APPEARS IN
संबंधित प्रश्न
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
The diagonal of a rectangular plot is 34 m and its perimeter is 92 m. Find its area.
Trapezium given below; find its area.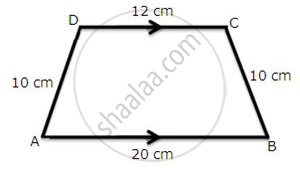
Calculate the area of quadrilateral ABCD in which AB = 32 cm, AD = 24 cm ∠A = 90° and BC = CD = 52 cm.
A wire when bent in the form of a square encloses an area of 484 m2. Find the largest area enclosed by the same wire when bent to from:
- An equilateral triangle.
- A rectangle of length 16 m.
The length and the breadth of a rectangle are 6 cm and 4 cm respectively. Find the height of a triangle whose base is 6 cm and the area is 3 times that of the rectangle.
The following diagram shows a pentagonal field ABCDE in which the lengths of AF, FG, GH, and HD are 50 m, 40 m, 15 m and 25 m, respectively, and the lengths of perpendiculars BF, CH and EG are 50 m, 25 m and 60 m respectively. Determine the area of the field.
Find the value of k, if the area of a quadrilateral is 28 sq. units, whose vertices are (– 4, – 2), (– 3, k), (3, – 2) and (2, 3)
The quadrilateral swimming pool shown is surrounded by concrete patio. Find the area of the patio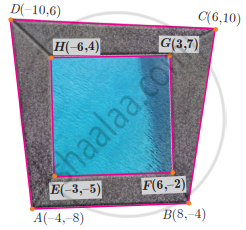
When proving that a quadrilateral is a trapezium, it is necessary to show
