Advertisements
Advertisements
प्रश्न
The cost of enclosing a rectangular garden with a fence all around, at the rate of 75 paise per metre, is Rs. 300. If the length of the garden is 120 metres, find the area of the field in square metres.
उत्तर
The perimeter of the garden
s = `300/0.75` = 400 sq .m
Again, the length of the garden is given to be 120 m. hence breadth of the garden b is given by
2( l + b ) = S
2 ( 120 + b ) = 400
b = 80m
Hence area of the field
A = 120 x 80
= 9600 sq . m
APPEARS IN
संबंधित प्रश्न
The diagonal of a rectangular plot is 34 m and its perimeter is 92 m. Find its area.
The area of a parallelogram is y cm2 and its height is h cm. The base of another parallelogram is x cm more than the base of the first parallelogram and its area is twice the area of the first. Find, in terms of y, h, and x, the expression for the height of the second parallelogram.
Trapezium given below; find its area.

The figure given below shows the cross-section of a concrete structure. Calculate the area of cross-section if AB = 1.8 cm, CD = 0.6 m, DE = 0.8 m, EF = 0.3 m and AF = 1.2 m.
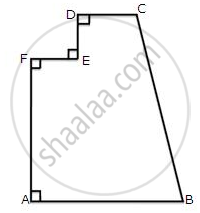
The shaded region of the given diagram represents the lawn in the form of a house. On the three sides of the lawn, there are flowerbeds having a uniform width of 2 m.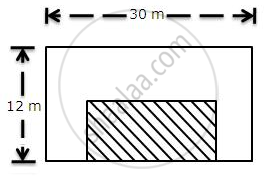
(i) Find the length and the breadth of the lawn.
(ii) Hence, or otherwise, find the area of the flower-beds.
Sum of the areas of two squares is 400 cm2. If the difference of their perimeters is 16 cm, find the sides of the two squares.
Find the area of the quadrilateral whose vertices are at (– 9, 0), (– 8, 6), (– 1, – 2) and (– 6, – 3)
The quadrilateral swimming pool shown is surrounded by concrete patio. Find the area of the patio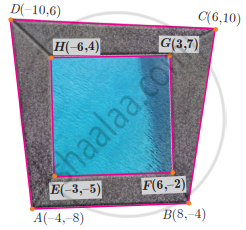
When proving that a quadrilateral is a parallelogram by using slopes you must find
PQRS is a rectangle formed by joining the points P(– 1, – 1), Q(– 1, 4), R(5, 4) and S(5, – 1). A, B, C and D are the mid-points of PQ, QR, RS and SP respectively. Is the quadrilateral ABCD a square, a rectangle or a rhombus? Justify your answer.
