Advertisements
Advertisements
प्रश्न
If the diagonal d of a quadrilateral is doubled and the heights h1 and h2 falling on d are halved, then the area of quadrilateral is ______.
उत्तर
If the diagonal d of a quadrilateral is doubled and the heights h1 and h2 falling on d are halved, then the area of quadrilateral is `underlinebb(1/2(h_1 + h_2)d)`.
Explanation:
Let ABCD be a quadrilateral, where h1 and h2 are altitudes on the diagonal BD = d.
Then, area of quadrilateral ABCD = `1/2(h_1 + h_2) xx BD`
If altitudes are halved and the diagonal is doubled, then
Area of quadrilateral ABCD = `1/2(h_1/2 + h_2/2) xx 2d`
= `1/2((h_1 + h_2)/2) xx 2d`
= `1/2(h_1 + h_2) xx d`
APPEARS IN
संबंधित प्रश्न
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
The diagonals of a quadrilateral are 16 cm and 13 cm. If they intersect each other at right angles; find the area of the quadrilateral.
Calculate the area of quadrilateral ABCD, in which ∠ABD = 90°, triangle BCD is an equilateral triangle of side 24 cm and AD = 26 cm.
Trapezium given below; find its area.
A rectangular plot 85 m long and 60 m broad is to be covered with grass leaving 5 m all around. Find the area to be laid with grass.
The perimeter of a rhombus is 46 cm. If the height of the rhombus is 8 cm; find its area.
A floor that measures 15 m x 8 m is to be laid with tiles measuring 50 cm x 25 cm. Find the number of tiles required.
Further, if a carpet is laid on the floor so that a space of 1 m exists between its edges and the edges of the floor, what fraction of the floor is left uncovered?
The shaded region of the given diagram represents the lawn in the form of a house. On the three sides of the lawn, there are flowerbeds having a uniform width of 2 m.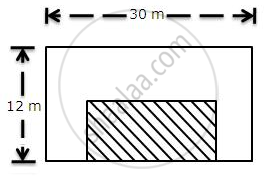
(i) Find the length and the breadth of the lawn.
(ii) Hence, or otherwise, find the area of the flower-beds.
Find the area of a quadrilateral field whose sides are 12m, 9m, 18m and 21m respectively and the angle between the first two sides is a right angle. Take the value of `sqrt(6)` as 2.5.
Let P(11, 7), Q(13.5, 4) and R(9.5, 4) be the midpoints of the sides AB, BC and AC respectively of ∆ABC. Find the coordinates of the vertices A, B and C. Hence find the area of ∆ABC and compare this with area of ∆PQR.
