Advertisements
Advertisements
प्रश्न
Find the area of a quadrilateral field whose sides are 12m, 9m, 18m and 21m respectively and the angle between the first two sides is a right angle. Take the value of `sqrt(6)` as 2.5.
उत्तर
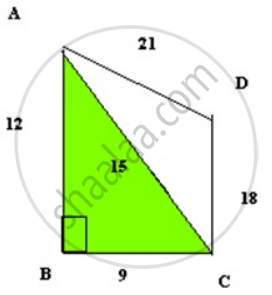
In the given quadrilateral ABCD, join diagonal AC
ABC is a right triangle
We know that, Area of a Triangle = `(1)/(2)"b.h" "i.e" (1)/(2)("Base" xx "Height")`
Area of a Triangle ABC = `(1)/(2)9.12` = 54m2
AC is the hypotenuse, AC
= `sqrt(12^2 + 9^2)`
= `sqrt(225)`
= 15m
Triangle ACD has sides 15m, 18m, 21m
We know that, Area of a Triangle whose sides are a, b, and c and semiperimeter is s is given by `sqrt("s"("s" - "a")("s" - "b")("s" -"c")); "s" = ("a" + "b" + "c")/(2)`
For a triangle whose sides are cm, cm and cm
i.e a = 15, b = 18 and c = 21,
s = `(15 + 18 + 21)/(2)`
= `(54)/(2)`
= 27
Area
= `sqrt(27(27 - 15)(27 - 18)(27 - 21)`
= `sqrt(27(12)(9)(6)`
= `sqrt(9 xx 3(6 xx 2)(9)(6)`
= `9 xx 6sqrt(6)`
= `54sqrt(6)`
= 54(2.5)
Area(Quad ABCD) = Ar(Triangle ABC) + Ar(Triangle ADC)
54 + 54(2.5)
= 54(1 + 2.5)
= 54(3.5)
= 189m2.
APPEARS IN
संबंधित प्रश्न
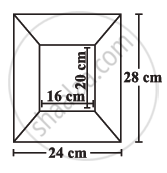
Diagram of the adjacent picture frame has outer dimensions = 24 cm × 28 cm and inner dimensions 16 cm × 20 cm. Find the area of each section of the frame, if the width of each section is same.
ABCD is a square with each side 12 cm. P is a point on BC such that area of ΔABP: area of trapezium APCD = 1: 5. Find the length of CP.
The length of a rectangle is twice the side of a square and its width is 6 cm greater than the side of the square. If the area of the rectangle is three times the area of the square; find the dimensions of each.
The figure given below shows the cross-section of a concrete structure. Calculate the area of cross-section if AB = 1.8 cm, CD = 0.6 m, DE = 0.8 m, EF = 0.3 m and AF = 1.2 m.
The width of a rectangular room is `4/7`of its length, x, and its perimeter is y. Write an equation connecting x and y. Find the length of the room when the perimeter is 4400 cm.
The perimeter of a rhombus is 52 cm. If one diagonal is 24 cm; find:
(i) The length of its other diagonal,
(ii) Its area.
Sum of the areas of two squares is 400 cm2. If the difference of their perimeters is 16 cm, find the sides of the two squares.
Find the area of the quadrilateral whose vertices are at (– 9, – 2), (– 8, – 4), (2, 2) and (1, – 3)
PQRS is a rectangle formed by joining the points P(– 1, – 1), Q(– 1, 4), R(5, 4) and S(5, – 1). A, B, C and D are the mid-points of PQ, QR, RS and SP respectively. Is the quadrilateral ABCD a square, a rectangle or a rhombus? Justify your answer.
If the diagonal d of a quadrilateral is doubled and the heights h1 and h2 falling on d are halved, then the area of quadrilateral is ______.
