Advertisements
Advertisements
प्रश्न
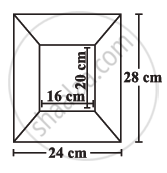
Diagram of the adjacent picture frame has outer dimensions = 24 cm × 28 cm and inner dimensions 16 cm × 20 cm. Find the area of each section of the frame, if the width of each section is same.
उत्तर
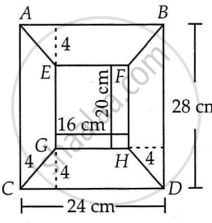
Area of ABFE
= `1/2` (AB + EF) × 4 cm2
= `1/2` (24 + 16) × 4 cm2
= `1/2` × 40 × 4 cm2
= 80 cm2
Also, Area of GHDC = Area of ABFE
= 80 cm2
Area of AEGC = `1/2` (EG + AC) × 4cm2
= `1/2 (20 + 28)` × 4cm2
= 96 cm2
Also, Area of AEGC = BFHD = 96 cm2 Area of EFHG
= HG × HF
= 16 × 20 cm2
= 320 cm2
APPEARS IN
संबंधित प्रश्न
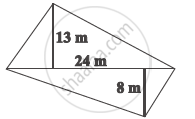
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
ABCD is a square with each side 12 cm. P is a point on BC such that area of ΔABP: area of trapezium APCD = 1: 5. Find the length of CP.
The length of a rectangle is twice the side of a square and its width is 6 cm greater than the side of the square. If the area of the rectangle is three times the area of the square; find the dimensions of each.
The perimeter of a rectangular board is 70 cm. Taking its length as x cm, find its width in terms of x.
If the area of the rectangular board is 300 cm2; find its dimensions.
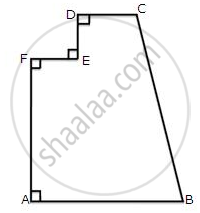
The figure given below shows the cross-section of a concrete structure. Calculate the area of cross-section if AB = 1.8 cm, CD = 0.6 m, DE = 0.8 m, EF = 0.3 m and AF = 1.2 m.
Two adjacent sides of a parallelogram are 24 cm and 18 cm. If the distance between the longer sides is 12 cm; find the distance between the shorter sides.
In the following, find the value of ‘a’ for which the given points are collinear
(a, 2 – 2a), (– a + 1, 2a) and (– 4 – a, 6 – 2a)
Find the value of k, if the area of a quadrilateral is 28 sq. units, whose vertices are (– 4, – 2), (– 3, k), (3, – 2) and (2, 3)
If vertices of a quadrilateral are at A(– 5, 7), B(– 4, k), C(– 1, – 6) and D(4, 5) and its area is 72 sq. units. Find the value of k.
If the diagonal d of a quadrilateral is doubled and the heights h1 and h2 falling on d are halved, then the area of quadrilateral is ______.
