Advertisements
Advertisements
प्रश्न
Find the area of the quadrilateral whose vertices are at (– 9, – 2), (– 8, – 4), (2, 2) and (1, – 3)
उत्तर
Let the vertices A(– 9, – 2), B(– 8, – 4), C(2, 2) and D(1, – 3).
Plot the vertices in a graph.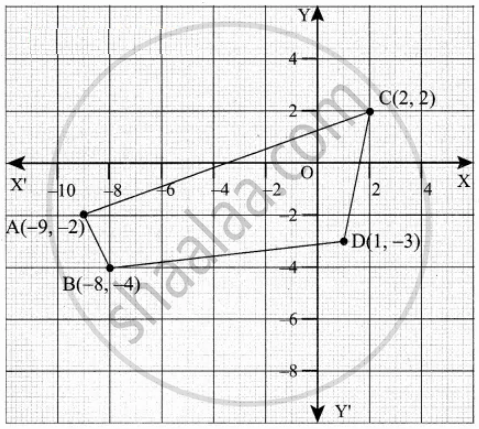
Note: Consider the points in counter clockwise order
Area of the Quadrilateral = `1/2[(x_1y_2 + x_2y_3 + x_3y_4 + x_4y_1) - (x_2y_1 + x_3y_2 + x_4y_3 + x_1y_4)]`

Area of the Quadrilateral ABDC = `1/2[36 + 24 + 2 - 4 - (16 - 4 - 6 - 18)]`
= `1/2[58 - (- 12)] - 1/2 [58 + 12]`
= `1/2 xx 70`
= 35 sq.units
Area of the Quadrilateral = 35 sq.units
APPEARS IN
संबंधित प्रश्न
The area of a parallelogram is y cm2 and its height is h cm. The base of another parallelogram is x cm more than the base of the first parallelogram and its area is twice the area of the first. Find, in terms of y, h, and x, the expression for the height of the second parallelogram.
Trapezium given below; find its area.
A wire when bent in the form of a square encloses an area of 484 m2. Find the largest area enclosed by the same wire when bent to from:
- An equilateral triangle.
- A rectangle of length 16 m.
Sum of the areas of two squares is 400 cm2. If the difference of their perimeters is 16 cm, find the sides of the two squares.
The perimeter of a semicircular plate is 108 cm. find its area.
Find the area of a quadrilateral field whose sides are 12m, 9m, 18m and 21m respectively and the angle between the first two sides is a right angle. Take the value of `sqrt(6)` as 2.5.
Find the diagonal of a quadrilateral whose area is 756cm2 and the perpendicular from the opposite vertices are 17cm and 19cm.
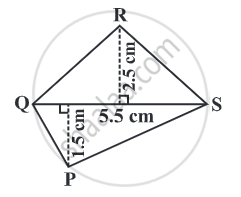
Find the area of quadrilateral PQRS.
When proving that a quadrilateral is a trapezium, it is necessary to show
If the diagonal d of a quadrilateral is doubled and the heights h1 and h2 falling on d are halved, then the area of quadrilateral is ______.
