Advertisements
Advertisements
प्रश्न
Find the area of the quadrilateral whose vertices are at (– 9, – 2), (– 8, – 4), (2, 2) and (1, – 3)
उत्तर
Let the vertices A(– 9, – 2), B(– 8, – 4), C(2, 2) and D(1, – 3).
Plot the vertices in a graph.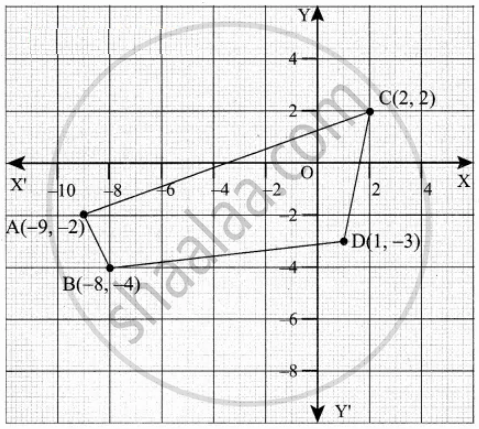
Note: Consider the points in counter clockwise order
Area of the Quadrilateral = `1/2[(x_1y_2 + x_2y_3 + x_3y_4 + x_4y_1) - (x_2y_1 + x_3y_2 + x_4y_3 + x_1y_4)]`

Area of the Quadrilateral ABDC = `1/2[36 + 24 + 2 - 4 - (16 - 4 - 6 - 18)]`
= `1/2[58 - (- 12)] - 1/2 [58 + 12]`
= `1/2 xx 70`
= 35 sq.units
Area of the Quadrilateral = 35 sq.units
APPEARS IN
संबंधित प्रश्न
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
The diagonals of a quadrilateral are 16 cm and 13 cm. If they intersect each other at right angles; find the area of the quadrilateral.
The perimeter of a rhombus is 46 cm. If the height of the rhombus is 8 cm; find its area.
The perimeter of a rhombus is 52 cm. If one diagonal is 24 cm; find:
(i) The length of its other diagonal,
(ii) Its area.
The area of a rhombus is 216 sq. cm. If it's one diagonal is 24 cm; find:
(i) Length of its other diagonal,
(ii) Length of its side,
(iii) The perimeter of the rhombus.
A triangle and a parallelogram have the same base and the same area. If the side of the triangle is 26 cm, 28 cm, and 30 cm and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
The perimeter of a semicircular plate is 108 cm. find its area.
When proving that a quadrilateral is a trapezium, it is necessary to show
When proving that a quadrilateral is a parallelogram by using slopes you must find
If the diagonal d of a quadrilateral is doubled and the heights h1 and h2 falling on d are halved, then the area of quadrilateral is ______.
