Advertisements
Advertisements
प्रश्न
The perimeter of a rectangular plot is 300m. It has an area of 5600m2. Taking the length of the plot as x m, calculate the breadth of the plot in terms of x, form an equation and solve it to find the dimensions of the plot.
उत्तर
The length of the rectangle = x m
Let the breadth of the rectangle = b m
The perimeter of a rectangle with length l and breadth b = P = 2(l + b)
The perimeter of a triangle with length x and breadth b = 2(x + b) = 300
⇒ (x + b) = 150
⇒ b = 150 - x
The area of a rectangle with length l and breadth b = A = l x b
The area of a rectangle with length x and breadth (150 - x)
= X x (150 - x)
= 5600
⇒150x - x2 = 5600
⇒ x2 - 150x + 5600 = 0
⇒ x2 - 80x - 70x + 5600 = 0
⇒ x(x - 80) - 70(x - 80) = 0
⇒ (x - 80)(x - 70) = 0
⇒ x = 70m, 80m
When breadth = 70m, then the length
= 150 - 70
= 80m
When breadth = 80m, then the length
= 150 - 80
= 70m.
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle with ∠ABD = 40°. Determine ∠DBC .
State, 'true' or 'false'
If the diagonals of a quadrilateral bisect each other at right angle, the quadrilateral is a square.
In the following figure, AE and BC are equal and parallel and the three sides AB, CD, and DE are equal to one another. If angle A is 102o. Find angles AEC and BCD.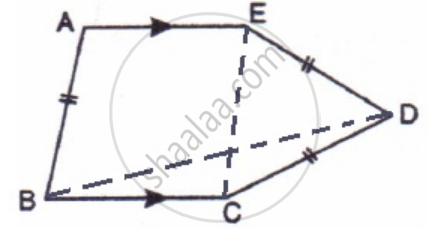
The given figure shows a square ABCD and an equilateral triangle ABP. 
Calculate: (i) ∠AOB
(ii) ∠BPC
(iii) ∠PCD
(iv) Reflex ∠APC
ABCD is a parallelogram having an area of 60cm2. P is a point on CD. Calculate the area of ΔAPB.
PQRS is a rectangle in which PQ = 12cm and PS = 8cm. Calculate the area of ΔPRS.
In the given figure area of ∥ gm PQRS is 30 cm2. Find the height of ∥ gm PQFE if PQ = 6 cm.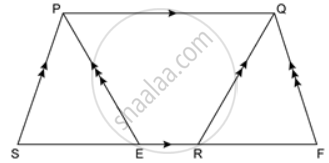
In the given figure, PQRS is a ∥ gm. A straight line through P cuts SR at point T and QR produced at N. Prove that area of triangle QTR is equal to the area of triangle STN.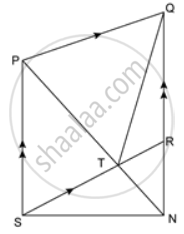
In the given figure, ST ∥ PR. Prove that: area of quadrilateral PQRS = area of ΔPQT.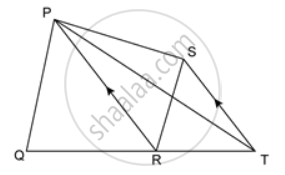
In the figure, PQR is a straight line. SQ is parallel to Tp. Prove that the quadrilateral PQST is equal in area to the ΔPSR.
The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in P and CD in Q. Show that
(a) Area of APQD = `(1)/(2)` area of || gm ABCD
(b) Area of APQD = Area of BPQC
Two adjacent sides of a parallelogram are 20cm and 18cm. If the distance between the larger sides is 9cm, find the area of the parallelogram. Also, find the distance between the shorter sides.
The length of a rectangular field is thrice of its width. If the perimeter of this field is 1.6km, find its area in sq.m.
Find the perimeter of a rhombus whose diagonals are 24cm and 10cm.
Find the area of a rhombus whose perimeter is 260cm and the length of one of its diagonal is 66cm.
Inside a square field of side 44m, a square flower bed is prepared leaving a graved path all round the flower bed. The total cost of laying the flower bed at Rs.25per sq m. and gravelling the path at Rs.120per sq m. is Rs.80320. Find the width of the gravel path.
All the sides of a rhombus are of equal length.
Give reasons for the following :
A square can be thought of as a special rhombus.
