Advertisements
Advertisements
प्रश्न
Two adjacent sides of a parallelogram are 20cm and 18cm. If the distance between the larger sides is 9cm, find the area of the parallelogram. Also, find the distance between the shorter sides.
उत्तर
Area of a parallelogram with base b and height h is A = b x h
∴ Area of a parallelogram with base 20cm and height 9cm is A = 20 x 9 = 180cm2
The height corresponding to the side 18cm = xcm
Area of a parallelogram with base 18cm and height xcm is A = 18 x x
⇒ 20 x 9 = 18 x x
⇒ x = `(20 xx 9)/(18)`
= 10cm.
APPEARS IN
संबंधित प्रश्न
Diagonal AC of a parallelogram ABCD bisects ∠A (see the given figure). Show that
- It bisects ∠C also,
- ABCD is a rhombus

ABCD is a trapezium in which AB || CD and AD = BC (see the given figure). Show that
- ∠A = ∠B
- ∠C = ∠D
- ΔABC ≅ ΔBAD
- diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
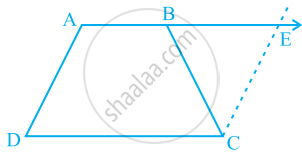
State, 'true' or 'false'
The diagonals of a rectangle bisect each other.
In parallelogram ABCD, AP and AQ are perpendiculars from the vertex of obtuse angle A as shown.
If ∠x: ∠y = 2: 1.
find angles of the parallelogram.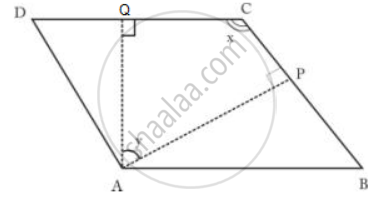
State, 'true' or 'false'
Every parallelogram is a rhombus.
In the following figures, ABCD is a parallelogram.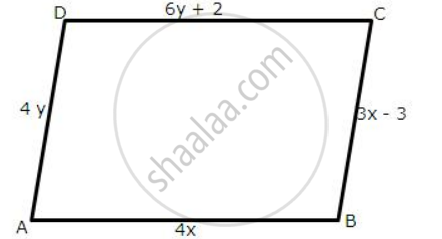
find the values of x and y.
In the figure, PT is parallel to SR. QTSR is a parallelogram and PQSR is a rectangle. If the area of ΔQTS is 60cm2, find:
(i) the area o || gm QTSR
(ii) the area of the rectangle PQRS
(iii) the area of the triangle PQS.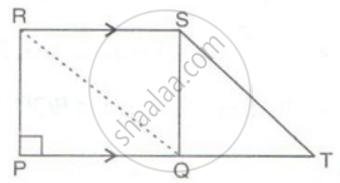
In the given figure area of ∥ gm PQRS is 30 cm2. Find the height of ∥ gm PQFE if PQ = 6 cm.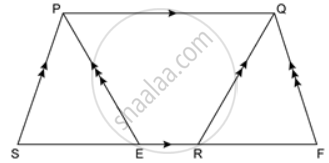
In the given figure, ST ∥ PR. Prove that: area of quadrilateral PQRS = area of ΔPQT.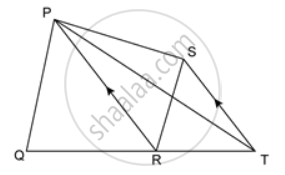
The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in P and CD in Q. Show that
(a) Area of APQD = `(1)/(2)` area of || gm ABCD
(b) Area of APQD = Area of BPQC
Prove that the median of a triangle divides it into two triangles of equal area.
In the given figure, ABC is a triangle and AD is the median.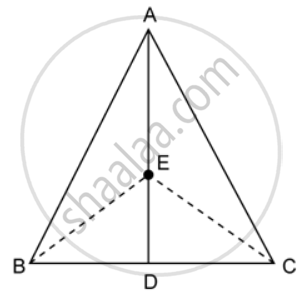
If E is any point on the median AD. Show that: Area of ΔABE = Area of ΔACE.
Find the perimeter and area of a rectangle whose length and breadth are 12cm and 9cm respectively.
The area of a floor of a rectangular room is 360m2. If its length is 24cm, find its perimeter.
Find the perimeter and area of a square whose diagonal is `5sqrt(2)"cm"`. Give your answer correct to two decimal places if `sqrt(2)` = 1.414.
The side of a square exceeds the side of another square by 4cm and the sum of the areas of the squares is 400cm2. Find the dimensions of the squares.
In quadrilateral ABCD, ∠A + ∠D = 180º. What special name can be given to this quadrilateral?
Each angle of a rectangle is a right angle.
Give reasons for the following :
A rectangle can be thought of as a special parallelogram.
