Advertisements
Advertisements
प्रश्न
The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in P and CD in Q. Show that
(a) Area of APQD = `(1)/(2)` area of || gm ABCD
(b) Area of APQD = Area of BPQC
उत्तर
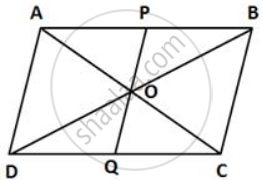
(a) A diagonal divides a parallelogram into two triangles of equal areas.
⇒ A(ΔADB) = `(1)/(2)`A(|| gm ABCD) ....(i)
In ΔDOQ and ΔBOP,
∠DOQ = ∠BOP ...(Vertically opposite angles)
DO = BO ...(Diagonals of a || gm bisect each other)
∠ODQ = ∠OBP ...(Alternate angles)
∴ ΔDOQ ≅ ΔBOP ...(ASA test of congruency)
⇒ A(ΔDOQ) = A(ΔBOP)
Adding A(DOQ) on both sides, we get
A(ΔDOQ) + A(DOPA) = A(ΔBOP) + A(DOPA)
⇒ Area of APQD = A(ADB)
⇒ Area of APQD = `(1)/(2)`A(|| gm ABCD) [From (i)] ....(ii)
(b) A(ΔABC) = `(1)/(2)`A(|| gm ABCD)
In ΔCOQ and ΔAOP,
∠COQ = ∠AOP ...(Vertically opposite angles)
CCO = AO ...(Diagonals of a || gm bisect each other)
∠OCQ = ∠OAP ...(Alternate angles)
∴ ΔCOQ ≅ ΔAOP ...(ASA test of congruency)
⇒ A(ΔCOQ) = A(ΔAOP)
Adding A(COPB) on both sides, we get
A(ΔCOQ) + A(COPB) = A(ΔAOP) + A(COPB)
∴ Area of BPQC = A(ABC)
⇒ Area of BPQC = `(1)/(2)`A(|| gm ABCD) ....(iii)
∴ Area of APQD = Area of BPQC. ...[From (ii) and (iii)]
APPEARS IN
संबंधित प्रश्न
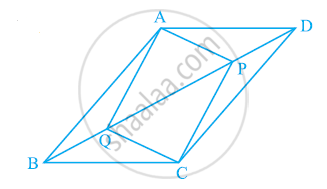
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see the given figure). Show that:
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ is a parallelogram
State, 'true' or 'false'
The quadrilateral, whose four sides are equal, is a square.
The angles of a quadrilateral are in the ratio 3: 4: 5: 6. Show that the quadrilateral is a trapezium.
In the following figures, ABCD is a parallelogram.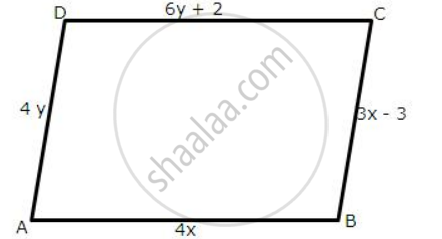
find the values of x and y.
State, 'true' or 'false'
If two adjacent sides of a parallelogram are equal, it is a rhombus.
In the following figure, AE and BC are equal and parallel and the three sides AB, CD, and DE are equal to one another. If angle A is 102o. Find angles AEC and BCD.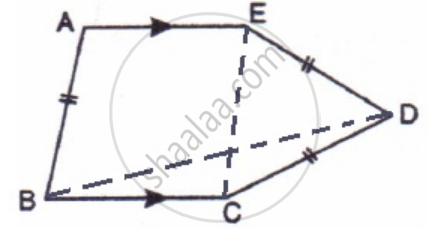
In the figure, ABCD is a parallelogram and APD is an equilateral triangle of side 80cm, Calculate the area of parallelogram ABCD.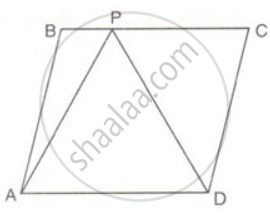
In the figure, PQR is a straight line. SQ is parallel to Tp. Prove that the quadrilateral PQST is equal in area to the ΔPSR.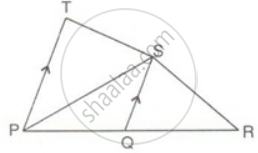
In a rectangle ABCD, AB = 7 cm and AD = 25 cm. Find the height of a triangle whose base is AB and whose area is two times the area of the rectangle ABCD.
Find the perimeter and area of a rectangle whose length and breadth are 12cm and 9cm respectively.
A rectangular floor 45 in long and 12 m broad is to be paved exactly with square tiles, of side 60 cm. Find the total number of tiles required to pave it.
If a carpet is laid on the floor such as a space of 50 cm exists between its edges and the edges of the floor, find what fraction of the floor is uncovered.
Find the perimeter and area of a square whose diagonal is `5sqrt(2)"cm"`. Give your answer correct to two decimal places if `sqrt(2)` = 1.414.
The area of a rhombus is 234 cm2. If its one diagonal is 18 cm, find the lengths of its side and the other diagonal. Also, find perimeter of the rhombus.
A rectangular field is 80m long and 50m wide. A 4m wide runs through the centre of the field parallel to the length and breadth of the field. Find the total area of the roads.
Inside a square field of side 44m, a square flower bed is prepared leaving a graved path all round the flower bed. The total cost of laying the flower bed at Rs.25per sq m. and gravelling the path at Rs.120per sq m. is Rs.80320. Find the width of the gravel path.
A footpath of uniform width runs all around the inside of a rectangular garden of 40 m x 30 m. If the path occupies 136 m2, find the width of the path.
PQRS is a square with each side 6cm. T is a point on QR such that the `"area of ΔPQT"/"area of trapezium PTRS" = (1)/(3)` Find the length of TR.
Give reason for the following :
Squares, rectangles, parallelograms are all quadrilaterals.
Examine whether the following is a polygon. If it is not, say why?

Examine whether the following is a polygon. If it is not, say why?

