Advertisements
Advertisements
प्रश्न
In the figure, PQR is a straight line. SQ is parallel to Tp. Prove that the quadrilateral PQST is equal in area to the ΔPSR.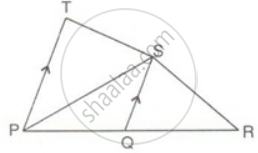
उत्तर
In quadrilateral PQST,
ar(ΔPQS) = `(1)/(2)` x ar(quadrilateral PQST)
ar(quadrilateral PQST) = 2ar(ΔPQS) .......(i)
In ΔPSR,
ar(ΔPSR) = ar(ΔPQS) + ar(ΔQSR)
but ar(ΔPQS) = ar(ΔQSR) ...(since QS is median as QS || TP)
ar(ΔPSR) = 2ar(ΔPQS) ........(ii)
From (i) and (ii)
ar(quadrilateral PQST) = ar(ΔPSR).
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
- ABCD is a square
- diagonal BD bisects ∠B as well as ∠D.
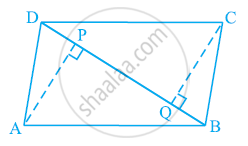
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure). Show that
- ΔAPB ≅ ΔCQD
- AP = CQ
State, 'true' or 'false'
The diagonals of a rectangle bisect each other.
State, 'true' or 'false'
The diagonals of a parallelogram bisect each other at right angle.
State, 'true' or 'false'
The quadrilateral, whose four sides are equal, is a square.
In the figure, given below, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that: ∠AMD = 90°.

In the given figure ABCD is a rhombus with angle A = 67°

If DEC is an equilateral triangle, calculate:
- ∠CBE
- ∠DBE
In the figure, ABCD is a parallelogram and APD is an equilateral triangle of side 80cm, Calculate the area of parallelogram ABCD.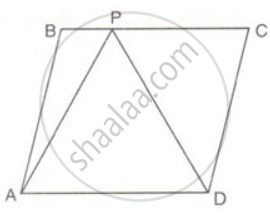
AD is a median of a ΔABC.P is any point on AD. Show that the area of ΔABP is equal to the area of ΔACP.
If the medians of a ΔABBC intersect at G, show that ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) = `(1)/(3)"ar(ΔABC)"`.
Find the area of each of the following figure:
Find the area of a parallelogram whose base is 12cm and the height is 5cm.
The length of a rectangular field is thrice of its width. If the perimeter of this field is 1.6km, find its area in sq.m.
A rectangular field 240m long has an area 36000m2. Find the cost of fencing the field at Rs.2.50per m.
The area of a square garden is equal to the area of a rectangular plot of length 160m and width 40m. Calculate the cost of fencing the square garden at Rs.12per m.
PQRS is a square with each side 6cm. T is a point on QR such that the `"area of ΔPQT"/"area of trapezium PTRS" = (1)/(3)` Find the length of TR.
ABCD is a trapezium in which AB || DC and ∠A = ∠B = 45º. Find angles C and D of the trapezium.
All the sides of a parallelogram are of equal length.
Name polygon.
Make two more examples of this.
