Advertisements
Advertisements
प्रश्न
ABCD is a trapezium in which AB || DC and ∠A = ∠B = 45º. Find angles C and D of the trapezium.
उत्तर
Given, ABCD is a trapezium and whose parallel sides in the figure are AB and DC.
Since, AB || CD and BC is transversal, then sum of two cointerior angles is 180°.
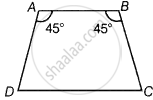
∴ ∠B + ∠C = 180º
⇒ ∠C = 180º – ∠B = 180º – 45º ...[∵ ∠B = 45º given]
⇒ ∠C = 135º
Similarly, ∠A + ∠D = 180º ...[Sum of cointerior angles is 180º]
⇒ ∠D = 180º – 45º ...[∵ ∠A = 45º given]
⇒ ∠D = 135º
Hence, angles C and D are 135º each.
APPEARS IN
संबंधित प्रश्न
Diagonal AC of a parallelogram ABCD bisects ∠A (see the given figure). Show that
- It bisects ∠C also,
- ABCD is a rhombus

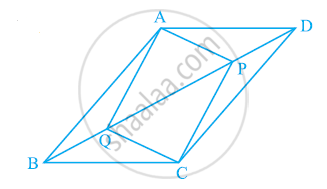
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see the given figure). Show that:
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ is a parallelogram
In the following figures, ABCD is a parallelogram.

Find the values of x and y.
In the figure, given below, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that: ∠AMD = 90°.

In a square ABCD, diagonals meet at O. P is a point on BC such that OB = BP.
Show that:
- ∠POC = `[ 22 ( 1°)/( 2 ) ]`
- ∠BDC = 2 ∠POC
- ∠BOP = 3 ∠CPO
In the figure, PT is parallel to SR. QTSR is a parallelogram and PQSR is a rectangle. If the area of ΔQTS is 60cm2, find:
(i) the area o || gm QTSR
(ii) the area of the rectangle PQRS
(iii) the area of the triangle PQS.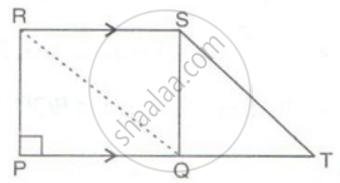
If the medians of a ΔABBC intersect at G, show that ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) = `(1)/(3)"ar(ΔABC)"`.
Find the area of each of the following figure:
The perimeter of a rectangular plot is 300m. It has an area of 5600m2. Taking the length of the plot as x m, calculate the breadth of the plot in terms of x, form an equation and solve it to find the dimensions of the plot.
Each angle of a rectangle is a right angle.
