Advertisements
Advertisements
प्रश्न
The angle between two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 60º. Find the angles of the parallelogram.
Advertisements
उत्तर
In quadrilateral DPBQ:
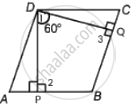
∠1 + ∠2 + ∠B + ∠3 = 360° ...[Angle sum property of quadrilateral]
60° + 90° + ∠B + 90° = 360°
∠B + 240° = 360°
∠B = 360° – 240°
∠B = 120°
Since, ∠ADC = ∠B = 120° ...[Opposite angles of a parallelogram are equal]
∠A + ∠B = 180° ...[Sum of consecutive interior angle is 180°]
∠A + 120° = 180°
∠A = 180° – 120°
∠A = 60°
So, ∠C = ∠A = 60° ...[Opposite angle of a parallelogram are equal]
APPEARS IN
संबंधित प्रश्न
Find the angle measure x in the given Figure
Find x + y + z
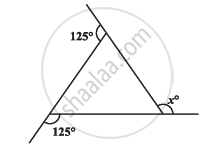
Find x in the following figures.
In Fig. below, ABCD is a parallelogram in which ∠DAB = 75° and ∠DBC = 60°. Compute
∠CDB and ∠ADB.
In a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB = 75°, then write the value of ∠C + ∠D.
In the given figure, PQRS is a rhombus in which the diagonal PR is produced to T. If ∠SRT = 152°, find x, y and z.
In the given figure, ABCD is a rectangle in which diagonal AC is produced to E. If ∠ECD = 146°, find ∠AOB.
If the degree measures of the angles of quadrilateral are 4x, 7x, 9x and 10x, what is the sum of the measures of the smallest angle and largest angle?
Sum of all the angles of a quadrilateral is 180°.
In a quadrilateral PQRS, ∠P = 50°, ∠Q = 50°, ∠R = 60°. Find ∠S. Is this quadrilateral convex or concave?
