Advertisements
Advertisements
प्रश्न
All the angles of a quadrilateral are equal. What special name is given to this quadrilateral?
उत्तर
We know that, sum of all angles in a quadrilateral is 360°.
If ABCD is a quadrilateral,
∠A + ∠B + ∠C + ∠D = 360° ...(i)
But it is given all angles are equal.
∠A = ∠B = ∠C = ∠D
From equation ...(i)
∠A + ∠A + ∠A + ∠A = 360°
⇒ 4∠A = 360°
∠A = 90°
So, all angles of a quadrilateral are 90°.
Hence, given quadrilateral is a rectangle.
APPEARS IN
संबंधित प्रश्न
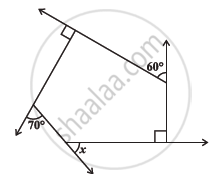
Find x in the following figures.
If an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram .
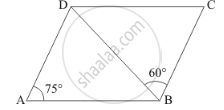
In Fig. below, ABCD is a parallelogram in which ∠DAB = 75° and ∠DBC = 60°. Compute
∠CDB and ∠ADB.
If an angle of a parallelogram is two-third of its adjacent angle, the smallest angle of the parallelogram is
If the diagonals of a rhombus are 18 cm and 24 cm respectively, then its side is equal to
In a rhombus ABCD, if ∠ACB = 40°, then ∠ADB =
The diagonals AC and BD of a rectangle ABCD intersect each other at P. If ∠ABD = 50°, then ∠DPC =
In the following figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. Prove that AD = 2CD.

The sum of all ______ of a quadrilateral is 360°.
Three angles of a quadrilateral are equal. Fourth angle is of measure 120°. What is the measure of equal angles?
