Advertisements
Advertisements
प्रश्न
In a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB = 75°, then write the value of ∠C + ∠D.
उत्तर
The quadrilateral can be drawn as follows:
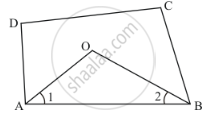
We have AO and BO as the bisectors of angles ∠A and ∠B respectively.
In ΔAOB,We have,
∠AOB + ∠1 +∠2 = 180°
∠AOB = 180° -(∠1 +∠2 )
∠AOB = 180° -`(1/2∠A + 1/2 ∠B)`
∠AOB = 180° - `1/2(∠A +∠B)` …… (1)
By angle sum property of a quadrilateral, we have:
∠A + ∠B +∠C + ∠D = 360°
∠A+ ∠B = 360° -(∠C +∠D)
Putting in equation (1):
`∠AOB =180° - 1/2[360° - (∠C + ∠D )]`
`∠AOB = 180° - 180° +(∠C +∠D)/2]`
`∠AOB = 1/2 (∠C +∠D)` ……(2)
It is given that ∠AOB = 75° in equation (2), we get:
`75° = 1/2 (∠C +∠D)`
`1/2(∠C+∠D) = 75°`
∠C + ∠D = 150°
Hence, the sum of ∠Cand ∠D is 150°.
APPEARS IN
संबंधित प्रश्न
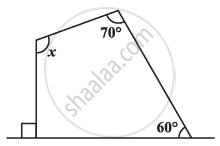
Find the angle measure x in the given Figure

Find x + y + z + w
The angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13 Find all the angles of the quadrilateral.
Two opposite angles of a parallelogram are (3x – 2)° and (50 – x)°. Find the measure of each angle of the parallelogram .
If an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram .
ABCD is a parallelogram in which ∠A = 70°. Compute ∠B, ∠C and ∠D .
The two diagonals are equal in a
The angle between two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 60º. Find the angles of the parallelogram.
In the following figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. Prove that AD = 2CD.

Three angles of a quadrilateral are equal. Fourth angle is of measure 120°. What is the measure of equal angles?
