Advertisements
Advertisements
Question
In a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB = 75°, then write the value of ∠C + ∠D.
Solution
The quadrilateral can be drawn as follows:
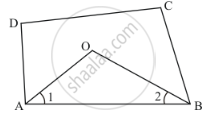
We have AO and BO as the bisectors of angles ∠A and ∠B respectively.
In ΔAOB,We have,
∠AOB + ∠1 +∠2 = 180°
∠AOB = 180° -(∠1 +∠2 )
∠AOB = 180° -`(1/2∠A + 1/2 ∠B)`
∠AOB = 180° - `1/2(∠A +∠B)` …… (1)
By angle sum property of a quadrilateral, we have:
∠A + ∠B +∠C + ∠D = 360°
∠A+ ∠B = 360° -(∠C +∠D)
Putting in equation (1):
`∠AOB =180° - 1/2[360° - (∠C + ∠D )]`
`∠AOB = 180° - 180° +(∠C +∠D)/2]`
`∠AOB = 1/2 (∠C +∠D)` ……(2)
It is given that ∠AOB = 75° in equation (2), we get:
`75° = 1/2 (∠C +∠D)`
`1/2(∠C+∠D) = 75°`
∠C + ∠D = 150°
Hence, the sum of ∠Cand ∠D is 150°.
APPEARS IN
RELATED QUESTIONS
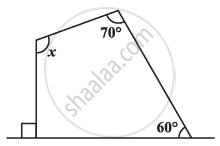
Find the angle measure x in the given Figure

Find x + y + z + w
Three angles of a quadrilateral are respectively equal to 110°, 50° and 40°. Find its fourth angle
In a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1 : 2 : 4 : 5. Find the measure of each angles of the quadrilateral
Diagonals necessarily bisect opposite angles in a
If the degree measures of the angles of quadrilateral are 4x, 7x, 9x and 10x, what is the sum of the measures of the smallest angle and largest angle?
The diagonals AC and BD of a rectangle ABCD intersect each other at P. If ∠ABD = 50°, then ∠DPC =
Which of the following can be four interior angles of a quadrilateral?
The angles P, Q, R and S of a quadrilateral are in the ratio 1:3:7:9. Then PQRS is a ______.
The polygon in which sum of all exterior angles is equal to the sum of interior angles is called ______.
