Advertisements
Advertisements
Question
Diagonals necessarily bisect opposite angles in a
Options
rectangle
parallelogram
isosceles trapezium
square
Solution
From the given choices, only in a square the diagonals bisect the opposite angles.
Let us prove it.
Take the following square ABCD with diagonal AD.
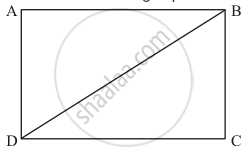
In ΔABD and ΔCBD:
AD = BC (Opposite sides of a square are equal.)
BD = BD (Common)
AB = DC (Opposite sides of a square are equal.)
Thus,
ΔABD ≅ ΔCBD (By SSS Congruence Rule)
By Corresponding parts of congruent triangles property we have:
∠ABD = ∠CBD
∠ADB = ∠CDB
Therefore, in a square the diagonals bisect the opposite angles.
Hence the correct choice is (d).
APPEARS IN
RELATED QUESTIONS
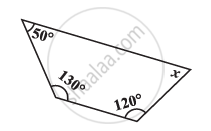
Find the angle measure x in the given Figure
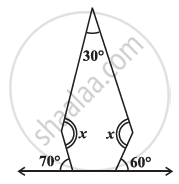
Find the angle measure x in the given Figure
In a quadrilateral ABCD, CO and DO are the bisectors of `∠`C and ∠D respectively. Prove that
`∠`COD = `1/2` (`∠`A+ `∠`B).
Two opposite angles of a parallelogram are (3x – 2)° and (50 – x)°. Find the measure of each angle of the parallelogram .
If the angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13, then find the measure of the smallest angle.
Can the angles 110º, 80º, 70º and 95º be the angles of a quadrilateral? Why or why not?
Can all the angles of a quadrilateral be right angles? Give reason for your answer.
In the following figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. Prove that AD = 2CD.

If three angles of a quadrilateral are each equal to 75°, the fourth angle is ______.
Sum of all the angles of a quadrilateral is 180°.
