Advertisements
Advertisements
प्रश्न
Diagonals necessarily bisect opposite angles in a
विकल्प
rectangle
parallelogram
isosceles trapezium
square
उत्तर
From the given choices, only in a square the diagonals bisect the opposite angles.
Let us prove it.
Take the following square ABCD with diagonal AD.
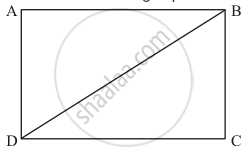
In ΔABD and ΔCBD:
AD = BC (Opposite sides of a square are equal.)
BD = BD (Common)
AB = DC (Opposite sides of a square are equal.)
Thus,
ΔABD ≅ ΔCBD (By SSS Congruence Rule)
By Corresponding parts of congruent triangles property we have:
∠ABD = ∠CBD
∠ADB = ∠CDB
Therefore, in a square the diagonals bisect the opposite angles.
Hence the correct choice is (d).
APPEARS IN
संबंधित प्रश्न
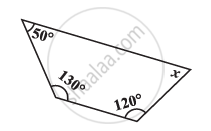
Find the angle measure x in the given Figure
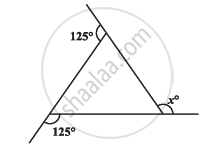
Find x in the following figure:
In a quadrilateral ABCD, CO and DO are the bisectors of `∠`C and ∠D respectively. Prove that
`∠`COD = `1/2` (`∠`A+ `∠`B).
In a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB = 75°, then write the value of ∠C + ∠D.
The diagonals of a rectangle ABCD meet at O, If ∠BOC = 44°, find ∠OAD.
In the given figure, PQRS is a rhombus in which the diagonal PR is produced to T. If ∠SRT = 152°, find x, y and z.

The figure formed by joining the mid-points of the adjacent sides of a square is a
The diagonals AC and BD of a rectangle ABCD intersect each other at P. If ∠ABD = 50°, then ∠DPC =
Can all the four angles of a quadrilateral be obtuse angles? Give reason for your answer.
In a quadrilateral PQRS, ∠P = 50°, ∠Q = 50°, ∠R = 60°. Find ∠S. Is this quadrilateral convex or concave?
