Advertisements
Advertisements
प्रश्न
In the given figure, PQRS is a rhombus in which the diagonal PR is produced to T. If ∠SRT = 152°, find x, y and z.

उत्तर
Rhombus PQRS is given.
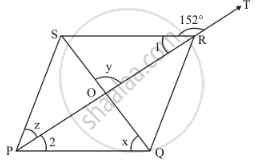
Diagonal PR is produced to T.
Also, ∠SRT = 152°.
We know that in a rhombus, the diagonals bisect each other at right angle.
Therefore,
y = 90°
Now,
∠1 + ∠SRT = 180°
∠1 +152° = 180°
∠1 = 28°
In ΔSOR, by angle sum property of a triangle, we get:
∠1 +y +∠OSR = 180°
28° +90° +∠OSR = 180°
118° +∠OSR = 180°
∠OSR = 62°
Or, ∠QSR = 62° (Because O lies on SQ)
We have, SP || PQ .Thus the alternate interior opposite angles must be equal.
Therefore,
x = ∠QSR
x = 62°
In ΔSPR,we have
Since opposite sides of a rhombus are equal.
Therefore,
PS = SR
Also,
Angles opposite to equal sides are equal.
Thus,
z = ∠1
But ∠1 = 28°
Thus, z = 20°
Hence the required values for x,y and z are 62°,90° and 28° respectively.
APPEARS IN
संबंधित प्रश्न
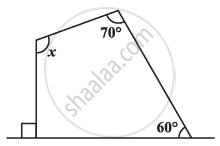
Find the angle measure x in the given Figure
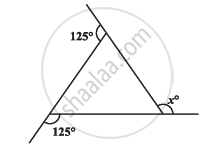
Find x in the following figure:
In a quadrilateral ABCD, CO and DO are the bisectors of `∠`C and ∠D respectively. Prove that
`∠`COD = `1/2` (`∠`A+ `∠`B).
If an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram .
PQRS is a square such that PR and SQ intersect at O. State the measure of ∠POQ.
If PQRS is a square, then write the measure of ∠SRP.
In a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB = 75°, then write the value of ∠C + ∠D.
In the given figure, ABCD is a rectangle in which diagonal AC is produced to E. If ∠ECD = 146°, find ∠AOB.
In a rhombus ABCD, if ∠ACB = 40°, then ∠ADB =
Can all the angles of a quadrilateral be acute angles? Give reason for your answer.
