Advertisements
Advertisements
Question
In the given figure, PQRS is a rhombus in which the diagonal PR is produced to T. If ∠SRT = 152°, find x, y and z.

Solution
Rhombus PQRS is given.
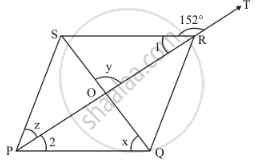
Diagonal PR is produced to T.
Also, ∠SRT = 152°.
We know that in a rhombus, the diagonals bisect each other at right angle.
Therefore,
y = 90°
Now,
∠1 + ∠SRT = 180°
∠1 +152° = 180°
∠1 = 28°
In ΔSOR, by angle sum property of a triangle, we get:
∠1 +y +∠OSR = 180°
28° +90° +∠OSR = 180°
118° +∠OSR = 180°
∠OSR = 62°
Or, ∠QSR = 62° (Because O lies on SQ)
We have, SP || PQ .Thus the alternate interior opposite angles must be equal.
Therefore,
x = ∠QSR
x = 62°
In ΔSPR,we have
Since opposite sides of a rhombus are equal.
Therefore,
PS = SR
Also,
Angles opposite to equal sides are equal.
Thus,
z = ∠1
But ∠1 = 28°
Thus, z = 20°
Hence the required values for x,y and z are 62°,90° and 28° respectively.
APPEARS IN
RELATED QUESTIONS
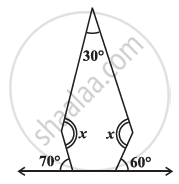
Find the angle measure x in the given Figure
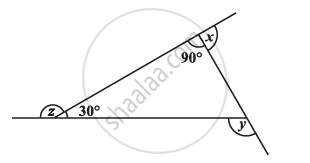
Find x + y + z

Find x + y + z + w
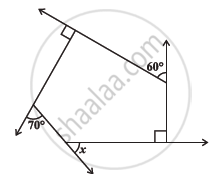
Find x in the following figures.
Three angles of a quadrilateral are respectively equal to 110°, 50° and 40°. Find its fourth angle
If an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram .
ABCD is a parallelogram in which ∠A = 70°. Compute ∠B, ∠C and ∠D .
Diagonals necessarily bisect opposite angles in a
If the degree measures of the angles of quadrilateral are 4x, 7x, 9x and 10x, what is the sum of the measures of the smallest angle and largest angle?
Can all the angles of a quadrilateral be right angles? Give reason for your answer.
