Advertisements
Advertisements
Question
Two opposite angles of a parallelogram are (3x – 2)° and (50 – x)°. Find the measure of each angle of the parallelogram .
Advertisements
Solution
We know that
Opposite sides of a parallelogram are equal
∴ 3x - 2 = 50 - x
⇒ 3x + x = 50 + 2
⇒ 4x = 52
⇒ x = 13°
∴(3x - 2)° = (3 × 13 - 2) = 37°
(50 - x)° = (50 -13°) = 37°
Adjacent angles of a parallelogram are supplementary
∴ x + 37 = 180°
∴ x = 180° - 37° = 143°
Hence, four angles are : 37°,143°, 37°,143°
APPEARS IN
RELATED QUESTIONS
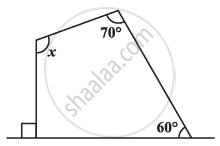
Find the angle measure x in the given Figure
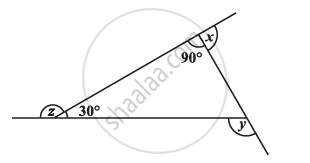
Find x + y + z
If an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram .
Can the angles 110º, 80º, 70º and 95º be the angles of a quadrilateral? Why or why not?
Can all the angles of a quadrilateral be acute angles? Give reason for your answer.
Can all the angles of a quadrilateral be right angles? Give reason for your answer.
The angle between two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 60º. Find the angles of the parallelogram.
The angles P, Q, R and S of a quadrilateral are in the ratio 1:3:7:9. Then PQRS is a ______.
Sum of all the angles of a quadrilateral is 180°.
Three angles of a quadrilateral are equal. Fourth angle is of measure 120°. What is the measure of equal angles?
