Advertisements
Advertisements
Question
The angle between two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 60º. Find the angles of the parallelogram.
Solution
In quadrilateral DPBQ:
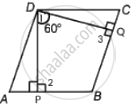
∠1 + ∠2 + ∠B + ∠3 = 360° ...[Angle sum property of quadrilateral]
60° + 90° + ∠B + 90° = 360°
∠B + 240° = 360°
∠B = 360° – 240°
∠B = 120°
Since, ∠ADC = ∠B = 120° ...[Opposite angles of a parallelogram are equal]
∠A + ∠B = 180° ...[Sum of consecutive interior angle is 180°]
∠A + 120° = 180°
∠A = 180° – 120°
∠A = 60°
So, ∠C = ∠A = 60° ...[Opposite angle of a parallelogram are equal]
APPEARS IN
RELATED QUESTIONS
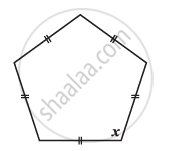
Find the angle measure x in the given Figure
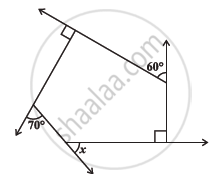
Find x in the following figures.
Find the measure of all the angles of a parallelogram, if one angle is 24° less than twice the smallest angle
In the given figure, PQRS is a rhombus in which the diagonal PR is produced to T. If ∠SRT = 152°, find x, y and z.

In the given figure, ABCD is a rectangle in which diagonal AC is produced to E. If ∠ECD = 146°, find ∠AOB.
If an angle of a parallelogram is two-third of its adjacent angle, the smallest angle of the parallelogram is
The diagonals AC and BD of a rectangle ABCD intersect each other at P. If ∠ABD = 50°, then ∠DPC =
All the angles of a quadrilateral are equal. What special name is given to this quadrilateral?
One angle of a quadrilateral is of 108º and the remaining three angles are equal. Find each of the three equal angles.
Sum of all the angles of a quadrilateral is 180°.
