Advertisements
Advertisements
Question
The diagonals AC and BD of a rectangle ABCD intersect each other at P. If ∠ABD = 50°, then ∠DPC =
Options
70°
90°
80°
100°
Solution
Figure can be drawn as follows:
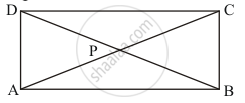
The diagonals AC and BD of rectangle ABCD intersect at P.
Also, it is given that ∠ABD = 50°
We need to find ∠DPC
It is given that∠ABD = 50°
Therefore, ∠ABP = 50°(Because P lies on BD)
Also, diagonals of rectangle are equal and they bisect each other.
Therefore,
AP = PB
Thus,∠ABP = ∠BAP (Angles opposite to equal sides are equal)
∠BAP = 50° [∠ABP = 50° (Given)]
By angle sum property of a triangle:
∠BAP + ∠ABP + ∠APB = 180°
50° + 50 +∠APB = 180°
100° + ∠APB = 180°
∠APB = 80°
But ∠APB and ∠DPC are vertically opposite angles.
Therefore, we get:
∠DPC = ∠APB
∠DPC = 80° [(∠APB = 80° lready proved)]
Hence the correct choice is (c).
APPEARS IN
RELATED QUESTIONS
Find the angle measure x in the given Figure
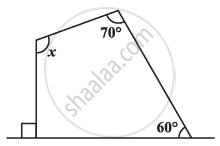
Find the angle measure x in the given Figure
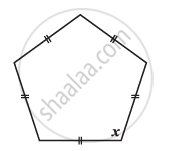
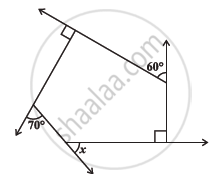
Find x in the following figures.
If an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram .
If PQRS is a square, then write the measure of ∠SRP.
In a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB = 75°, then write the value of ∠C + ∠D.
The diagonals of a rectangle ABCD meet at O, If ∠BOC = 44°, find ∠OAD.
In ΔABC, ∠A = 30°, ∠B = 40° and ∠C = 110°. The angles of the triangle formed by joining the mid-points of the sides of this triangle are
The angle between two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 60º. Find the angles of the parallelogram.
Three angles of a quadrilateral are equal. Fourth angle is of measure 120°. What is the measure of equal angles?
