Advertisements
Advertisements
Question
If PQRS is a square, then write the measure of ∠SRP.
Solution
The square PQRS is given as:
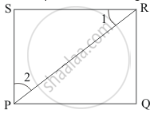
Since PQRS is a square.
Therefore,
PS = SR
and ∠PSR = 90°
Now, in ΔPSR, we have
PS = SR
That is, ∠1 = ∠2 (Angles opposite to equal sides are equal)
By angle sum property of a triangle.
∠PSR + ∠1 + ∠2 = 180°
∠PSR + 2∠1 = 180°
90° + 2∠1 = 180° (∠PSR = 90°)
2∠1 = 90°
∠1 = 45°
APPEARS IN
RELATED QUESTIONS
In a quadrilateral ABCD, CO and DO are the bisectors of `∠`C and ∠D respectively. Prove that
`∠`COD = `1/2` (`∠`A+ `∠`B).
If an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram .
PQRS is a square such that PR and SQ intersect at O. State the measure of ∠POQ.
In a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB = 75°, then write the value of ∠C + ∠D.
In the given figure, PQRS is a rhombus in which the diagonal PR is produced to T. If ∠SRT = 152°, find x, y and z.

The two diagonals are equal in a
All the angles of a quadrilateral are equal. What special name is given to this quadrilateral?
Can all the four angles of a quadrilateral be obtuse angles? Give reason for your answer.
In the following figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. Prove that AD = 2CD.

The polygon in which sum of all exterior angles is equal to the sum of interior angles is called ______.
