Advertisements
Advertisements
Question
In the following figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. Prove that AD = 2CD.

Solution
Given in the question, in a parallelogram ABCD, P is a mid-point of BC such that ∠BAP = ∠DAP.
To prove that AD = 2CD
Proof: ABCD is a parallelogram
So, AD || BC and AB is transversal, then
∠A + ∠B = 180° ...[Sum of cointerior angles is 180°]
∠B = 180° – ∠A ...(i)
Now, in triangle ABP,
∠PAB + ∠B + ∠BPA = 180° ...[By angle sum property of a triangle]
`1/2 ∠A + 180^circ - ∠A + ∠BPA = 180^circ` ...[From equation (i)]
`∠BPA - (∠A)/2 = 0`
`∠BPA = (∠A)/2` ...(ii)
∠BPA = ∠BAP
AB = BP ...[Opposite sides of equal angles are equal]
In above equation multiplying both side by 2, we get
2AB = 2BP
2AB = BC ...[P is the mid-point of BC]
2CD = AD ...[ABCD is a parallelogram, then AB = CD and BC = AD]
APPEARS IN
RELATED QUESTIONS
Find the angle measure x in the given Figure
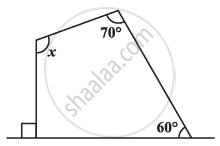
Find x in the following figure:
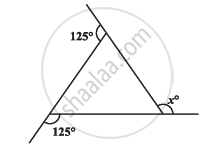
Three angles of a quadrilateral are respectively equal to 110°, 50° and 40°. Find its fourth angle
In a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1 : 2 : 4 : 5. Find the measure of each angles of the quadrilateral
If an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram .
Find the measure of all the angles of a parallelogram, if one angle is 24° less than twice the smallest angle
If the degree measures of the angles of quadrilateral are 4x, 7x, 9x and 10x, what is the sum of the measures of the smallest angle and largest angle?
In ΔABC, ∠A = 30°, ∠B = 40° and ∠C = 110°. The angles of the triangle formed by joining the mid-points of the sides of this triangle are
The angle between two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 60º. Find the angles of the parallelogram.
The angles P, Q, R and S of a quadrilateral are in the ratio 1:3:7:9. Then PQRS is a ______.
